Notes on Hainmueller, Mummolo & Xu: How Much Should we Trust Estimates from Multiplicative Interaction Models?

Part of my ongoing quest to replicate everything I see using the marginaleffects package.

Author

Vincent Arel-Bundock

Published

January 24, 2023

Political Scientists absolutely looove regression models with multiplicative interactions (Brambor, Clark, and Golder 2006; Braumoeller 2004). In “How Much Should we Trust Estimates from Multiplicative Interaction Models?” Hainmueller, Mummolo, and Xu (HMX) criticize the standard practice of entering these interactions linearly, and they propose two alternative strategies, using binning or kernel estimation (Hainmueller, Mummolo, and Xu 2019).

These two approaches are pretty straightforward to implement, but the specifications can be a little finicky to code up. And while the authors generously published an R package to implement their recommendations, the objects produced by this package are a little “non standard”, which makes them hard to use with packages to draw regression tables, etc.

These are my reading notes on HMX, showing how to estimate and interpret the recommended interaction models with standard R commands and the marginaleffects package. Very similar code could be used in Stata using the margins command.

To start, we load a few libraries:

library(mgcv)
library(ggplot2)
library(data.table)
library(marginaleffects)
set.seed(1024)

Simulated data

Consider this data generating process:

\[Y = 2.5 + -X^2 - 5 \cdot D + 2 \cdot D \cdot X^2 + \zeta,\]

with 1000 observations, \(X\sim U(-3,3)\), \(D\sim Bernoulli(.5)\), and \(\zeta\sim N(0, 2)\).

We can simulate a dataset which conforms to this process as follows:

N <- 1e3
FUN <- function(D, X) 2.5 - X^2 - 5 * D + 2 * D * X^2

dat <- data.table(
    X = runif(N, min = -3, max = 3),
    D = rbinom(N, size = 1, prob = .5),
    z = rnorm(N, mean = 0, sd = 2))[
    , truth := FUN(D, X)           ][
    , Y := truth + z               ]

head(dat)
            X     D          z      truth         Y
        <num> <int>      <num>      <num>     <num>
1: -1.6914650     1 -1.6435275  0.3610539 -1.282474
2:  2.9258055     1 -0.2248293  6.0603376  5.835508
3: -0.9092287     1  0.4060946 -1.6733032 -1.267209
4: -0.7137180     1 -1.7986797 -1.9906065 -3.789286
5: -2.8740842     1 -1.0910748  5.7603601  4.669285
6:  1.4983612     0  2.1108525  0.2549136  2.365766

The effect of \(D\) on \(Y\) depends on \(X\), and the moderating effect of \(X\) is non-linear. As such, fitting a simple model like this would probably generate less than useful results:

\[Y = \beta_0 + \beta_1 X + \beta_2 D + \beta_3 X\cdot D + \varepsilon\]

Indeed, a simple plot (HMX call this a “Linear Interaction Diagnostic Plot”) shows that the slope estimated by linear regression is essentially the same in the \(D=0\) and \(D=1\), even if the relationship is completely different:

ggplot(dat, aes(X, Y)) +
    geom_point(alpha = .2) +
    geom_smooth(se = FALSE, method = "lm", color = "#E69F00") +
    geom_smooth(se = FALSE, color = "#56B4E9") +
    facet_wrap(~ D)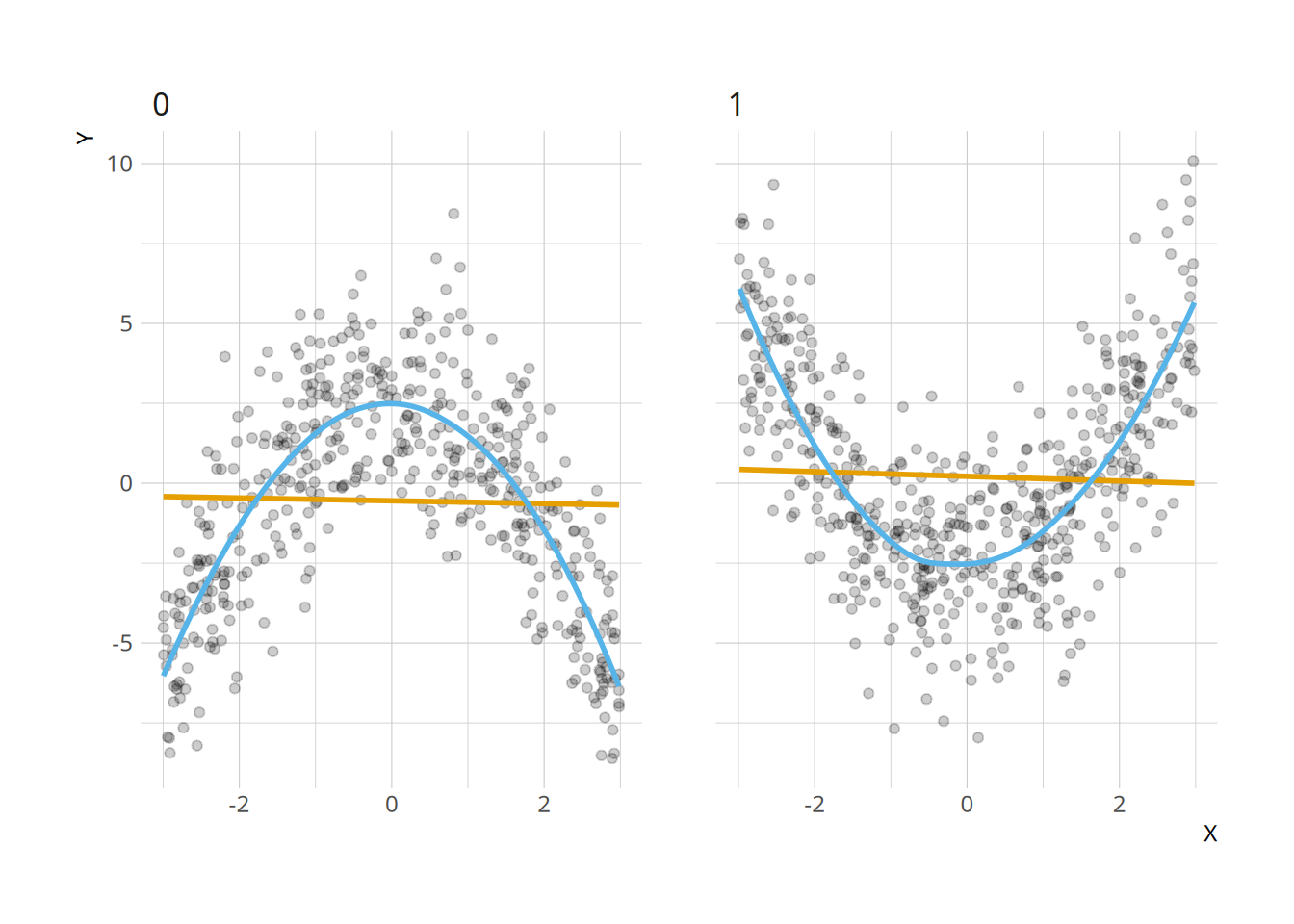

Bins

The first estimation strategy that HMX propose is reasonably simple: Split the moderator into bins, and estimate a model with carefully selected interactions and de-meaned (de-binned?) versions of the moderator. Say we decide to use 3 equal-sized bins. We then estimate:

\[Y = \sum_{j=1}^3 \{\mu_j + \alpha_j D + \eta_j (X-x_j) + \beta_j(X-x_j)D\}G_j + \varepsilon,\]

where \(x_j\) are the midpoints of each bin.

The clever thing about this specification is that the \(\alpha_j\) coefficients can immediately be interpreted as the marginal effects (partial derivatives) of \(D\) on \(Y\), when the moderator \(X\) is equal to \(x_1\), \(x_2\), or \(x_3\).

How would we do this in R? First, we create three bins on the moderator \(X\), and we calculate the midpoint value for each bin:

# create equal-sized bins 
bin <- seq(0, 1, length.out = 4)
dat[, bin := cut(X, quantile(X, prob = bin), include.lowest = TRUE)]

# midpoints of each bin
mid <- dat[, .(X = median(X), D = 0), by = "bin"]
dat <- merge(dat, mid[, .(mid = X, bin)])

Then, we estimate the model in the equation above using lm() and lots of parentheses and interaction terms:

lm(Y ~ (1 + D + I(X - mid) + D:I(X - mid)) : bin + bin,
   data = dat)

Call:
lm(formula = Y ~ (1 + D + I(X - mid) + D:I(X - mid)):bin + bin, 
    data = dat)

Coefficients:
                 (Intercept)                 bin(-1,0.978]               bin(0.978,2.98]                  D:bin[-3,-1]  
                     -1.9770                        4.1657                        0.3935                        3.6898  
             D:bin(-1,0.978]             D:bin(0.978,2.98]         I(X - mid):bin[-3,-1]      I(X - mid):bin(-1,0.978]  
                     -4.3717                        2.9852                        3.5812                       -0.2539  
  I(X - mid):bin(0.978,2.98]       D:I(X - mid):bin[-3,-1]    D:I(X - mid):bin(-1,0.978]  D:I(X - mid):bin(0.978,2.98]  
                     -4.1310                       -7.8325                        0.4824                        7.8430

Success! Three of the coefficients above correspond to the marginal effects (or slopes, or partial derivatives) we are looking for. But which ones, specifically? And did we include all the correct interaction terms? ¯\_(ツ)_/¯️

Here’s an alternative that I personally (100% subjective) find simpler:

  1. Interact everything.
  2. Call the the slopes() function (or margins, dydx at() in Stata) to compute marginal effects at the midpoints of each bin:
mod <- lm(Y ~ D * X * bin, data = dat)

slopes(mod,             # model with interactions
       variables = "D", # slope of Y with respect to D: dY/dD
       newdata = mid)   # values of the bin midpoints where we want to evaluate dY/dD

 Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
     3.69      0.225  16.4   <0.001 199.0  3.25   4.13
     2.99      0.225  13.3   <0.001 131.2  2.54   3.43
    -4.37      0.226 -19.4   <0.001 275.5 -4.81  -3.93

Term: D
Type:  response 
Comparison: 1 - 0
Columns: rowid, term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted, bin, X, D, Y

These are these are exactly the same results that we obtain with interflex, the package written by HMX:

library(interflex)
int <- interflex(
    Y = "Y",
    D = "D",
    X = "X",
    data = data.frame(dat),
    estimator = "binning",
    X.eval = mid$X)
Baseline group not specified; choose treat = 0 as the baseline group. 
int$est.bin[[1]]
                        x0      coef        sd  CI.lower  CI.upper
X:[-3,-1]      -2.06018891  3.689766 0.2269162  3.244473  4.135059
X:(-1,0.978]   -0.04869546 -4.371728 0.2189892 -4.801465 -3.941990
X:(0.978,2.98]  1.95675821  2.985156 0.2259654  2.541729  3.428584

Kernel estimator

In the next part of their paper, HMX recommend using a kernel estimator to more flexibly estimate the non-linear relationship between \(D\), \(X\), and \(Y\). Frankly, I did not read that section very attentively, and I don’t know exactly what kernel and cross-validation magic interflex does under the hood.

That said, it seems useful to know that there are tons of off-the-shelf software to estimate very flexible models with interactions and smooths. For example, a very simple GAM model can easily match the true data generating process simulated by HMX very closely. And since GAM-fitting packages like mgcv, are supported by marginaleffects, analysts can easily report useful quantities and plots.

First, estimate a GAM model with a smooth term of interaction between \(X\) and \(D\):

dat$D <- factor(dat$D)
mod <- gam(Y ~ s(X, by = D) + D, data = dat)

Estimate the average marginal effects for different values of \(X\) (the midpoints of the bins we used above):

avg_slopes(mod, by = "mid", variables = "D")

     mid Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 -2.0602     3.40      0.214  15.9   <0.001 185.6  2.98   3.82
 -0.0487    -4.40      0.205 -21.5   <0.001 338.8 -4.80  -4.00
  1.9568     3.26      0.215  15.2   <0.001 170.5  2.84   3.68

Term: D
Type:  response 
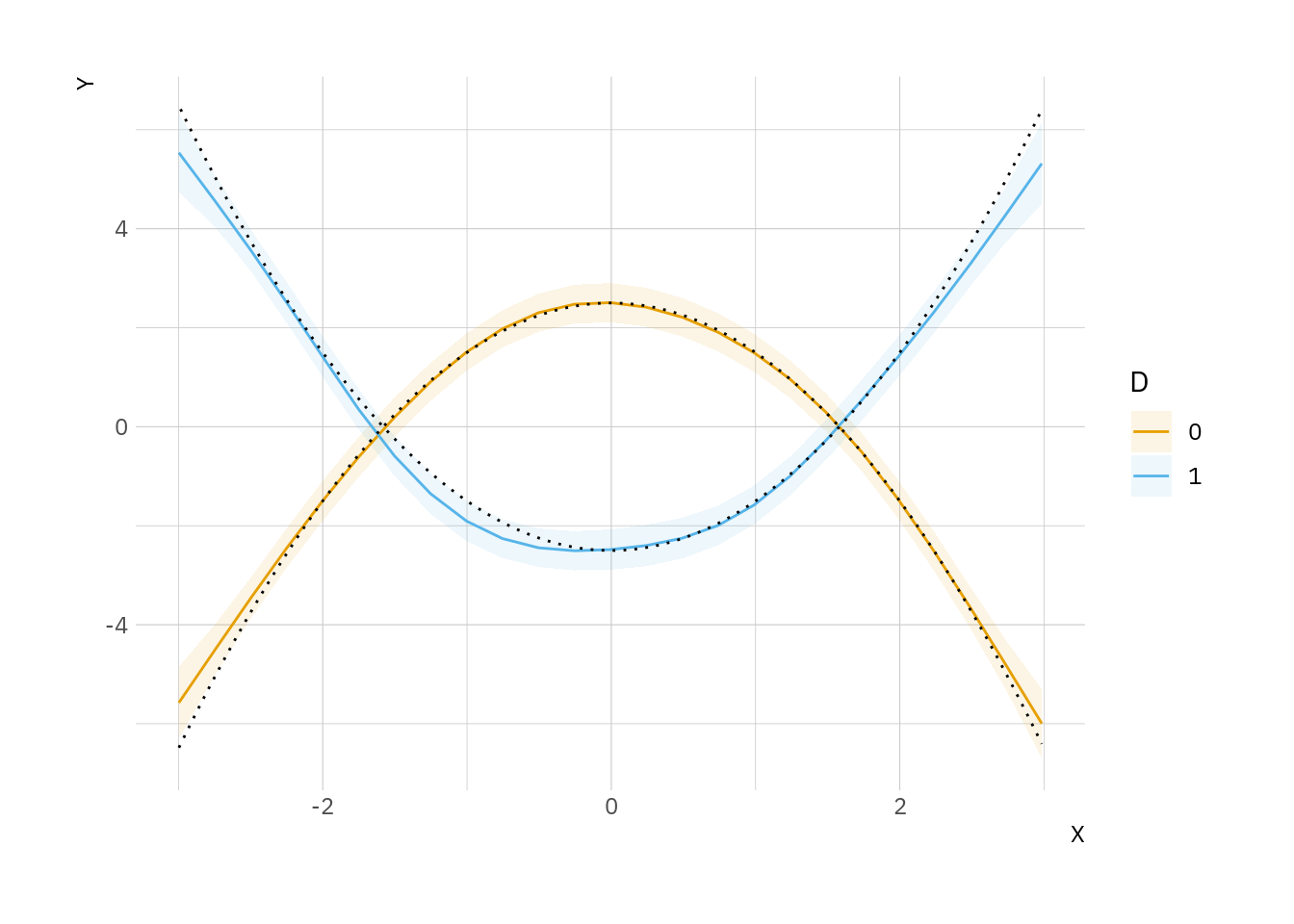
Comparison: mean(1) - mean(0)
Columns: term, contrast, mid, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted

Use the plot_predictions() function to plot the predictions of our GAM model against the true data generating process. Note that GAM (colors) predictions match the true curves (black dots) very closely:

plot_predictions(mod, condition = c("X", "D")) +
    geom_line(data = dat, aes(x = X, y = truth, group = D), linetype = 3)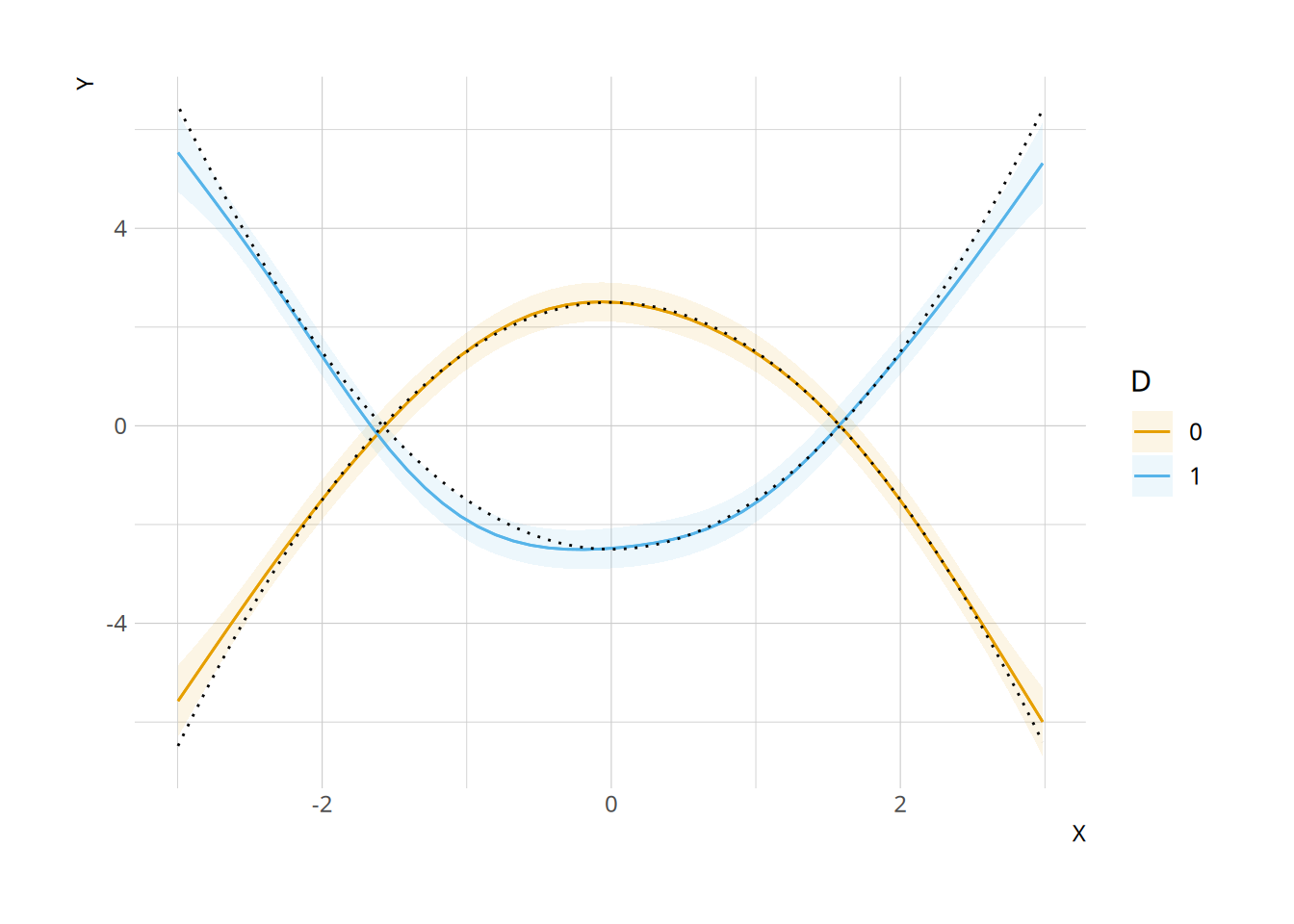

We can also use the plot_slopes() function to plot the marginal effects (\(\partial Y / \partial D\)) at different values of \(X\):

plot_slopes(mod, variables = "D", condition = "X")

References

Brambor, Thomas, William Roberts Clark, and Matt Golder. 2006. “Understanding Interaction Models: Improving Empirical Analyses.” Political Analysis 14 (1): 63–82.
Braumoeller, Bear F. 2004. “Hypothesis Testing and Multiplicative Interaction Terms.” International Organization 58 (4): 807–20.
Hainmueller, Jens, Jonathan Mummolo, and Yiqing Xu. 2019. “How Much Should We Trust Estimates from Multiplicative Interaction Models? Simple Tools to Improve Empirical Practice.” Political Analysis 27 (2): 163–92.