library(MASS)
library(ggplot2)
library(fabricatr)
library(patchwork)
library(DeclareDesign)
library(marginaleffects)My colleagues and I have argued that Quantitative Research in Political Science is Greatly Underpowered. Since we posted that paper, a lot of colleagues have asked me how big their sample needs to be to have sufficient statistical power. How many observations must one collect to have a good chance of rejecting the null hypothesis where it is false?
As always with such questions, the answer is: it depends. In theory, the appropriate sample size for a research project depends on the strength of the effect, the measurement instrument, the amount of noise, and numerous other features of the research design.
In practice, though, my honest answer to the “how big?” question is usually: “You need a bigger sample than you can afford.” Since the binding constraint in research design is often funding, I would argue that it is crucial to tackle this problem head-on, and integrate cost explicitly in sample size calculations and power analyses.
In this post, I illustrate how researchers can study the trade-off between money and power in research design. To do this, we will use the DeclareDesign package for R.
DeclareDesign is an extremely powerful package to conduct simulations and assess the properties of a research design: power, bias, RMSE, etc. The amount of flexibility afforded by DeclareDesign is impressive, but it necessarily comes with some complexity. To people like me, that complexity can feel intimidating.
This notebook strips out most of the package’s bells and whistles, and uses only its most basic functionality. I hope it will serve as both a self-contained introduction to DeclareDesign, and as a case study on the trade-off between money and power in research design.
Before jumping in, we load some R packages.
Two-Arm Randomized Controlled Trial
The first data generating process that we consider is an ultra-simple randomized experiment with binary treatment \(D\), outcome \(Y\), and noise \(\varepsilon\).
\[ Y = \beta_0 + \beta_1 D + \varepsilon \tag{1}\]
Our objective is to estimate the treatment effect \(\beta_1\), and to see how the statistical power of our research design varies as a function of sample size and treatment effects size.
To simulate data that conform to Equation 1, we call the declare_model() function. declare_model() is a convenience wrapper around the fabricate() function from the fabricatr package. It allows researchers to simulate very complex datasets, with hierarchical structures, weird sampling strategies, and complex treatment assignment schemes (e.g., blocks and/or clusters). In our case, the DGP is so simple that the code below is self-explanatory.
sample_size = 100
treatment_effect = 0.2
dgp = declare_model(
N = sample_size,
# standard normal noise
e = rnorm(N, mean = 0, sd = 1),
# random dummy treatment with equal probability of treatment and control
D = rbinom(N, size = 1, prob = 0.5),
# intercept
b0 = 0,
# outcome equation
Y = b0 + treatment_effect * D + e
)Our ultimate goal is to study how the statistical power of the research design varies when the sample size and treatment effect change. In DeclareDesign, the parameters that we intend to vary—like the sample_size and treatment_effect variables—must be defined before and outside the declare_model() call. See the code block above for an example.
declare_model() is what we call a “function factory”: it is a function that returns another function. Indeed, the dgp object that we created above can be called repeatedly to simulate new datasets from the same DGP.
Three rows from one simulation:
d = dgp()
head(d, 3) ID e D b0 Y
1 001 0.9583184 1 0 1.1583184
2 002 0.2680605 1 0 0.4680605
3 003 -0.8123032 1 0 -0.6123032Three different rows from another simulation:
d = dgp()
head(d, 3) ID e D b0 Y
1 001 -0.1160185 0 0 -0.1160185
2 002 1.9442361 0 0 1.9442361
3 003 -0.7943887 0 0 -0.7943887Now, we define a fit() function:
- Input:
- Data frame called
data
- Data frame called
- Output:
- 1-row data frame with mandatory and optional columns.
- Mandatory:
term,estimate - Optional:
std.error,conf.low,conf.high,p.value,cost, etc.
- Mandatory:
- 1-row data frame with mandatory and optional columns.
The fit() function defined below accepts a data frame, fits a linear regression model, and return a 1-row data frame as results.
fit = function(data) {
model = lm(Y ~ D, data = data)
out = data.frame(
"term" = "OLS",
"estimate" = coef(model)["D"]
)
return(out)
}
# simulate
d = dgp()
# estimate
fit(d) term estimate
D OLS 0.2589628Instead of extracting the estimates from the lm() model manually, we can use the avg_comparisons() function from the marginaleffects package. In this simple model, the estimate produced by avg_comparisons() will identical to the coefficient estimated by OLS. In more complex models, with interactions or non-linear components, avg_comparisons() will be a convenient way to estimate the average treatment effect (ATE), and to return results in the “tidy” format required by DeclareDesign.
fit = function(data) {
model = lm(Y ~ D, data = data)
out = avg_comparisons(model, variables = "D")
return(out)
}
fit(d) term contrast estimate std.error statistic p.value s.value conf.low conf.high predicted_lo predicted_hi predicted
1 D 1 - 0 0.2589628 0.1923981 1.345974 0.1783111 2.487532 -0.1181306 0.6360561 -0.07656265 0.1824001 -0.07656265Now, we use DeclareDesign to create an R object that represents a complete “research design”. This object is created by “adding” or “chaining” together calls to different DeclareDesign functions, using the + operator. In particular, we will call three functions:
declare_model()- Data generating process
declare_inquiry()- True value of the quantity of interest
declare_estimator()- Estimation procedure
Finally, once we have defined the research design, we can call the diagnose_design() function to assess its properties. This function will run simulations, estimate the treatment effect, and compute power, bias, etc.
Putting it all together:
library(DeclareDesign)
library(marginaleffects)
sample_size = 100
treatment_effect = 0.2
dgp = declare_model(
N = sample_size,
e = rnorm(N, mean = 0, sd = 1),
D = rbinom(N, size = 1, prob = 0.5),
Y = treatment_effect * D + e
)
estimator = declare_estimator(handler =
function(data) {
model = lm(Y ~ D, data = data)
out = avg_comparisons(model, variables = "D")
return(out)
}
)
truth = declare_inquiry(ATE = treatment_effect)
design = dgp + estimator + truth
diagnose_design(design)
Research design diagnosis based on 500 simulations. Diagnosis completed in 10 secs.
Design Inquiry Term Mean Estimand Mean Estimate Bias SD Estimate RMSE Power Coverage N Sims
design ATE D 0.20 0.20 0.00 0.21 0.21 0.18 0.95 500These simulation results suggest that our estimation strategy yields unbiased estimates. Unfortunately, the statistical power of our research design is very low.
Comparing DGPs
The statistical power of the research design we studied in the previous section is woefully low. To increase the power, we can increase the sample size, the treatment effect, or both.
To see this, we use the redesign() function from DeclareDesign to create a list of new research designs, with different combinations of effect and sample sizes. We then call the diagnose_design() function to compare the power of the different research designs.
design_list = redesign(design,
sample_size = c(100, 500),
treatment_effect = c(0.2, 0.5)
)
diagnose_design(design_list)
Research design diagnosis based on 500 simulations. Diagnosis completed in 9 secs.
Design sample_size treatment_effect Inquiry Term Mean Estimand Mean Estimate Bias SD Estimate RMSE Power Coverage N Sims
design_1 100 0.2 ATE D 0.20 0.21 0.01 0.20 0.20 0.19 0.94 500
design_2 500 0.2 ATE D 0.20 0.20 0.00 0.09 0.09 0.63 0.95 500
design_3 100 0.5 ATE D 0.50 0.51 0.01 0.20 0.20 0.72 0.97 500
design_4 500 0.5 ATE D 0.50 0.50 -0.00 0.09 0.09 1.00 0.96 500Clearly, designs with larger effect and/or sample sizes are better powered.
Comparing estimators
The data generating process that we consider follows this equation:
\[ Y = \beta_0 + \beta_1 D + \beta_2 X_1 + \beta_3 X_3 + \varepsilon, \]
where \(Y\) is the outcome, \(D\) a randomized binary treatment, \(X_1\) and \(X_2\) are covariates drawn from a multivariate normal distribution, and \(\varepsilon\) is a standard normal noise term.
sample_size = 100
treatment_effect = 0.2
dgp = declare_model(
N = sample_size,
e = rnorm(N, mean = 0, sd = 1),
D = rbinom(N, size = 1, prob = 0.5),
# random normal covariates
fabricatr::draw_multivariate(c(X1, X2) ~ MASS::mvrnorm(
n = N,
mu = c(0, 0),
Sigma = matrix(c(1, 0.5, 0.5, 1), 2, 2)
)),
Y = 1 + treatment_effect * D + 1 * X1 + 1 * X2 + e
)fit = function(data) {
# Linear model with regression adjustement for covariates
adjusted = lm(Y ~ D * (X1 + X2), data = data)
adjusted = avg_comparisons(adjusted, variables = "D", vcov = "HC3")
# Linear model with a single binary predictor
unadjusted = lm(Y ~ D, data = data)
unadjusted = avg_comparisons(unadjusted, variables = "D", vcov = "HC3")
# Combine the results
out = rbind(adjusted, unadjusted)
# Label the results
out$term = c("Adjusted", "Unadjusted")
return(out)
}We can fit this model directly to the output of dgp():
dgp() |> fit() term contrast estimate std.error statistic p.value s.value conf.low conf.high predicted_lo predicted_hi predicted
1 Adjusted 1 - 0 0.4346008 0.1838637 2.363711 0.0180929 5.788432 0.07423451 0.7949671 3.3696956 3.948897 3.948897
2 Unadjusted 1 - 0 0.5419386 0.4276202 1.267336 0.2050351 2.286057 -0.29618164 1.3800588 0.7817586 1.323697 1.323697And we can diagnose the research design as before:
truth = declare_inquiry(ATE = treatment_effect)
estimators = declare_estimator(handler = fit)
design = dgp + truth + estimators
diagnose_design(design)
Research design diagnosis based on 500 simulations. Diagnosis completed in 4 secs.
Design Inquiry Term Mean Estimand Mean Estimate Bias SD Estimate RMSE Power Coverage N Sims
design ATE Adjusted 0.20 0.19 -0.01 0.22 0.22 0.15 0.94 500
design ATE Unadjusted 0.20 0.16 -0.04 0.43 0.43 0.09 0.94 500Cost ($) vs. Power
In practice, the main constraint on research design is often the budget. To assess the trade-off between statistical power and cost, we start with the same data generating process as before:
library(DeclareDesign)
library(marginaleffects)
sample_size = 100
treatment_effect = 0.2
dgp = declare_model(
N = sample_size,
e = rnorm(N, mean = 0, sd = 1),
D = rbinom(N, size = 1, prob = 0.5),
Y = treatment_effect * D + e
)Now, we modify the declare_estimator() call used above, by adding a new column called cost to the output data frame. For each simulated dataset, this function will compute the total cost of data collection based on:
- Fixed data collection costs: 1000$
- Marginal cost of a unit in the treatment group: 10$
- Marginal cost of a unit in the control group: 5$
The cost of data collection will vary from dataset to dataset, depending on the number of units assigned to the treatment and control groups, and depending on the size of the datset we collect.
estimator = declare_estimator(handler =
function(data) {
# average treatment effect
model = lm(Y ~ D, data = data)
out = avg_comparisons(model, variables = "D")
# fixed cost
fixed = 1000
# marginal cost
marginal_0 = 5
marginal_1 = 10
# total cost
out$cost = fixed + sum(ifelse(data$D == 1, marginal_1, marginal_0))
return(out)
}
)Our goal is to contrast the statistical power of a design, to the maximum cost of dataset collection, for a range of potential sample sizes. DeclareDesign does not have a cost calculator built-in, so we must define one. In the language of DeclareDesign, the cost calculator is called a “diagnosand”, that is, a feature of the research design that we wish to diagnose.
To define diagnosands, we use the declare_diagnosands() function.
diagnosands = declare_diagnosands(
power = mean(p.value <= 0.05),
cost = max(cost)
)Finally, we build the design as before, and run simulations for many sample sizes.
truth = declare_inquiry(ATE = treatment_effect)
design = dgp + estimator + truth
design_list = redesign(
design,
sample_size = round(seq(100, 3000, length.out = 25))
)
results = diagnose_design(design_list, diagnosands = diagnosands)
p = results$diagnosands_df
par(mfrow = 1:2)
plot(power ~ sample_size, data = p, type = "l")
plot(cost ~ sample_size, data = p, type = "l")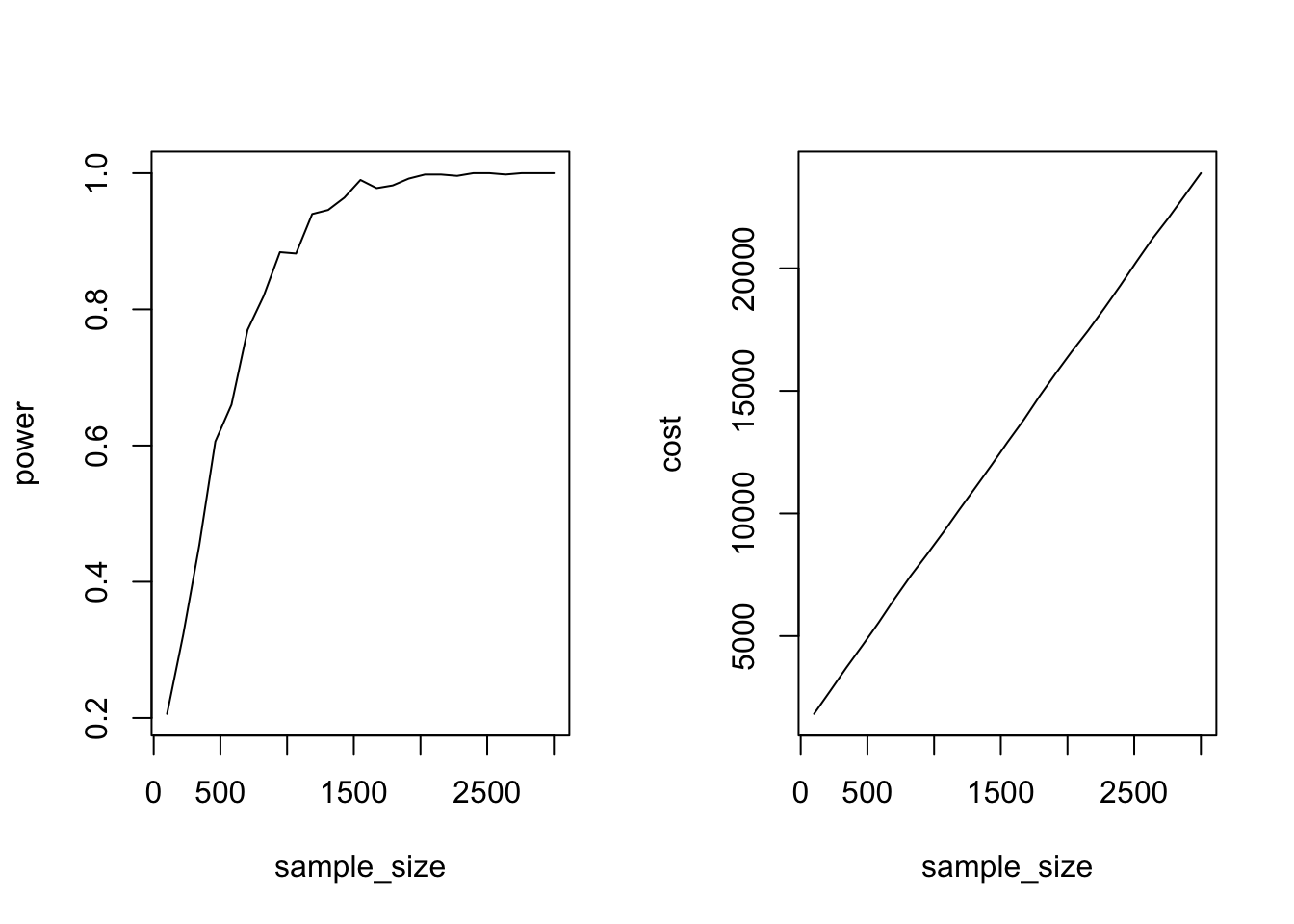
This graph shows that the costs increase linearly in sample size, but that the gains in terms of statistical power flatten out. After about 1500 observations, statistical power does not increase much anymore, even if we pour more money into data collection.