Frontdoor adjustment for causal inference: A primer with examples in R

Author

Vincent Arel-Bundock

Published

January 24, 2021

This notebook has 3 objectives:

  1. Offer some intuition about the “frontdoor” criterion and adjustment formula for causal inference.
  2. Show how to derive the frontdoor both algebraically and algorithmically using the dosearch package for R.
  3. Show how to apply the frontdoor adjustment formula in simulated data.

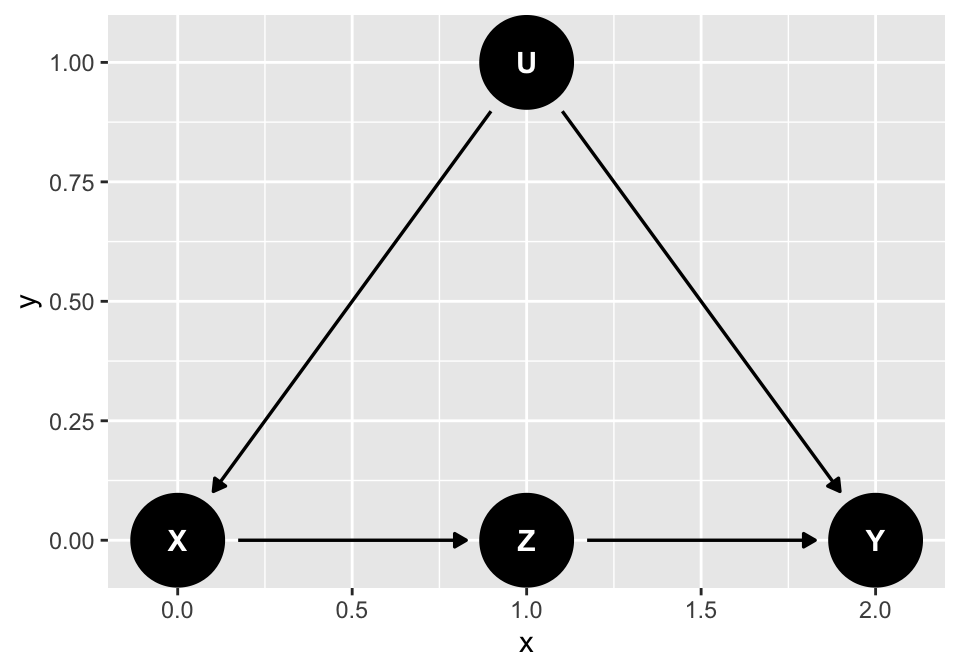
I assume that you know what a DAG and a backdoor path are.1 The data I will consider follows this data generating process, with a cause \(X\), a mediator \(Z\), an outcome \(Y\), and an unobserved confounder \(U\):

Pearl (2009) uses the \(do()\) operator to represent variables on which we intervene or that we manipulate.2 For instance, the expression \(P(Y|do(X=x))\) represents the distribution of the \(Y\) when we manipulate the treatment variable \(X\) to give it a specific value \(x\).

Our goal is to estimate \(P(Y|do(X))\). Unfortunately, this relationship between \(X\) and \(Y\) is confounded by the unobserved variable \(U\), via this backdoor path: \(X \leftarrow U \rightarrow Y\). Therefore, we cannot estimate the causal quantity of interest directly.

Instead, we will estimate the effect of \(X\) on \(Y\) indirectly via frontdoor adjustment. The key intuition behind this approach is this:

In a causal chain with three nodes \(X\rightarrow Z\rightarrow Y\), we can estimate the effect of \(X\) on \(Y\) indirectly by combining two distinct quantities: (1) an estimate of the effect of \(X\) on \(Z\), and (2) an estimate of the effect of \(Z\) on \(Y\).

Roughly speaking, frontdoor adjustment thus proceeds in 3 steps:

  1. Estimate \(P(Z|do(X))\)
  2. Estimate \(P(Y|do(Z),X)\)
  3. Combine the two

To illustrate these steps, I will use a simulated dataset that conforms to the DAG above, and where the true effect of \(X\) on \(Y\) is equal to 0.25:

library(data.table)
set.seed(731460)

N = 1e5
U = rbinom(N, 1, prob = .2)
X = rbinom(N, 1, prob = .1 + U * .6)
Z = rbinom(N, 1, prob = .3 + X * .5)
Y = rbinom(N, 1, prob = .1 + U * .3 + Z * .5)
dat = data.table(X, Z, Y)

In the simplest case, we can estimate the effect of \(X\) on \(Y\) by multiplying two linear regression coefficients.

Frist we estimate the effect of \(Z\) on \(X\). Since there is no open backdoor, we do not need to control for other variables:

step1 = lm(Z ~ X, dat)

Then, we estimate the effect of \(Z\) on \(Y\), controlling for \(X\) to close the backdoor:

step2 = lm(Y ~ Z + X, dat)

Finally, we combine the two estimates by multiplication:

coef(step1)["X"] * coef(step2)["Z"] 
        X 
0.2496002

Why did this produce the correct result (0.25)? To answer this question, we can use do-calculus to derive a frontdoor adjustment formula, or we can use an R package called dosearch to derive the formula automatically. The algorithmic approach is very useful in more complicated cases, but the algebraic approach helps us understand the assumptions that underlie the method.

Algebraic frontdoor

I borrow notation from a nice Cross Validated answer, and make the following assumptions:

  1. Full mediation: there is no directed path from \(X\) to \(Y\), except through \(Z\).
  2. Unconfoundedness 1: There is no open backdoor from \(X\) to \(Z\).
  3. Unconfoundedness 2: All backdoors from Z to Y are blocked by X.

The estimation proceeds in three steps.

Step 1: Under assumption 2, the relationship between \(X\) and \(Z\) is not confounded (see DAG at the top). As a result, we have:

\[ P(Z|do(X)) = P(Z|X) \]

Step 2: In contrast, the relationship between \(Z\) and \(Y\) is confounded. Thankfully, adjusting for \(X\) suffices to estimate the effect of \(Z\) on \(Y\), because it blocks the backdoor path. As a result, we can use the backdoor adjustment formula3 to get:

\[ P(Y|do(Z)) = \sum_{X}P(Y|X, Z) P(X) \]

Step 3: Back out the effect of \(X\) on \(Y\) by combining what we obtained above:

\[ \begin{aligned} P(Y|do(X)) &= \sum_{Z} P(Y|Z, do(X))P(Z|do(X)) && \mbox{(1)}\\ &= \sum_{Z} P(Y|do(Z))P(Z|do(X)) && \mbox{(2)}\\ &= \sum_{Z} P(Y|do(Z))P(Z|X) && \mbox{(3)}\\ &= \sum_{Z} \sum_{X}P(Y|X, Z) P(X)P(Z|X) && \mbox{(4)}\\ &= \sum_{Z}P(Z|X) \sum_{X}P(Y|X, Z) P(X) && \mbox{(5)} \end{aligned} \]

Equation (1) conditions on Z and sums over its values. Equation (2) is allowed because the effect of \(X\) is entirely mediated by \(Z\), and because \(X\) blocks the backdoor path from \(Z\) to \(Y\). Intuitively, if we manipulate \(Z\), it no longer matters what happened to \(X\). Equation (3) is allowed because the relationship between \(X\) and \(Z\) is unconfounded. Equation (4) applies the backdoor adjustment formula to estimate the effect of \(Z\) on \(Y\) by conditioning on \(X\).

Equation (5) is the frontdoor adjustment formula. The left part is the effect of \(X\) on \(Z\). The right part is the effect of \(Z\) on \(Y\).

Algorithmic frontdoor: R & dosearch

The dosearch package for R includes an algorithm that can automatically apply the rules of do-calculus to convert DAGs to adjustment formulas. Instead of manipulating equations ourselves like we did above, we can simply call the dosearch function to obtain the frontdoor adjustment formula automatically:

library('dosearch')

data1 = "P(X, Y, Z)"

query1 = "P(Y | do(X))"

graph1 = "
U -> X
U -> Y
X -> Z
Z -> Y
"

# compute
frontdoor = dosearch(data1, query1, graph1)

# convert to Rmarkdown equation
cat(paste("$$", frontdoor$formula, "$$"))

\[ \sum_{Z}\left(p(Z|X)\sum_{X}\left(p(X)p(Y|X,Z)\right)\right) \]

Which is equivalent to the formula we obtained above.

Example: Frontdoor simulation

With the frontdoor adjustment formula in hand, we can finally estimate the causal effect of \(X\) in our simulated data. We will work with this version fo the formula:

\[ P(Y|do(X)) = \sum_{Z}P(Z|X) \sum_{X}P(Y|X, Z) P(X) \]

dat[, `P(X)`     := fifelse(X == 1, mean(X), 1 - mean(X)) ][
    , `P(Z|X)`   := mean(Z), by = X                       ][
    , `P(Y|Z,X)` := mean(Y), by = .(Z, X)                 ][
    , `P(Z|X)`   := mean(Z), by = X                       ][
    , Y := NULL                                           ]
dat = unique(dat)
dat[, `P(Y|do(Z))` := sum(`P(Y|Z,X)` * `P(X)`), by = Z]

`P(Y|do(X=0))` = with(dat[X == 0], 
  `P(Z|X)`           [Z == 1] * 
  `P(Y|do(Z))`       [Z == 1] +
  (1 - `P(Z|X)`)     [Z == 0] * 
  `P(Y|do(Z))`       [Z == 0]
)

`P(Y|do(X=1))` = with(dat[X == 1], {
  `P(Z|X)`           [Z == 1] * 
  `P(Y|do(Z))`       [Z == 1] +
  (1 - `P(Z|X)`)     [Z == 0] * 
  `P(Y|do(Z))`       [Z == 0]
})

`P(Y|do(X=1))` - `P(Y|do(X=0))`
[1] 0.249766

As shown above, we can get essentially the same result using regression and multiplication:

coef(lm(Y ~ Z + X))["Z"] * coef(lm(Z ~ X))["X"]
        Z 
0.2496002

Or by estimating an impossible model (remember that \(U\) is unobservable):

coef(lm(Y ~ X + U))["X"]
        X 
0.2549541

References

Pearl, Judea. 2009. Causality. Cambridge university press.
Pearl, Judea, Madelyn Glymour, and Nicholas P Jewell. 2016. Causal Inference in Statistics: A Primer. John Wiley & Sons.

Footnotes

  1. Les lecteurs francophones peuvent se référer au chapitre 6 de mon livre “Analyse Causale et Méthodes Quantitatives”, disponible gratuitement en PDF: https://www.pum.umontreal.ca/catalogue/analyse_causale_et_methodes_quantitatives↩︎

  2. The manipulation could be hypothetical or counterfactual.↩︎

  3. See Pearl (2009) for a detailed treatment of backdoor adjustment, and Pearl, Glymour, and Jewell (2016) for an accessible primer.↩︎