This notebook introduces “Distribution Regression”, an alternative to quantile regression which can be used to explore treatment effect heterogeneity.
Warning: This notebook is not authoritative. These are essentially reading/coding notes, written as I was trying to figure this stuff out for myself. Please report mistakes and send me your comments.
Case study: restaurant inspections
To illustrate, we will use the restaurant inspections data used in Huntington-Klein (2022). These data are available in the causaldata package for R, or in the Rdatasets archive.
library(ggplot2)
library(marginaleffects)
library(modelsummary)
dat <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/causaldata/restaurant_inspections.csv")
head(dat) X business_name inspection_score Year NumberofLocations Weekend
1 1 MCGINLEYS PUB 94 2017 9 FALSE
2 2 VILLAGE INN #1 86 2015 66 FALSE
3 3 RONNIE SUSHI 2 80 2016 79 FALSE
4 4 FRED MEYER - RETAIL FISH 96 2003 86 FALSE
5 5 PHO GRILL 83 2017 53 FALSE
6 6 TACO KING #2 95 2008 89 FALSEOur goal is to check if there is a difference in the inspection scores when the inspection is conducted on a weekday or during the weekend, controlling for the year of inspection and the number of locations in the restaurant chain.
A first step can be to plot the empirical cumulative distribution function for those two groups:
ggplot(dat, aes(inspection_score, color = Weekend)) + stat_ecdf()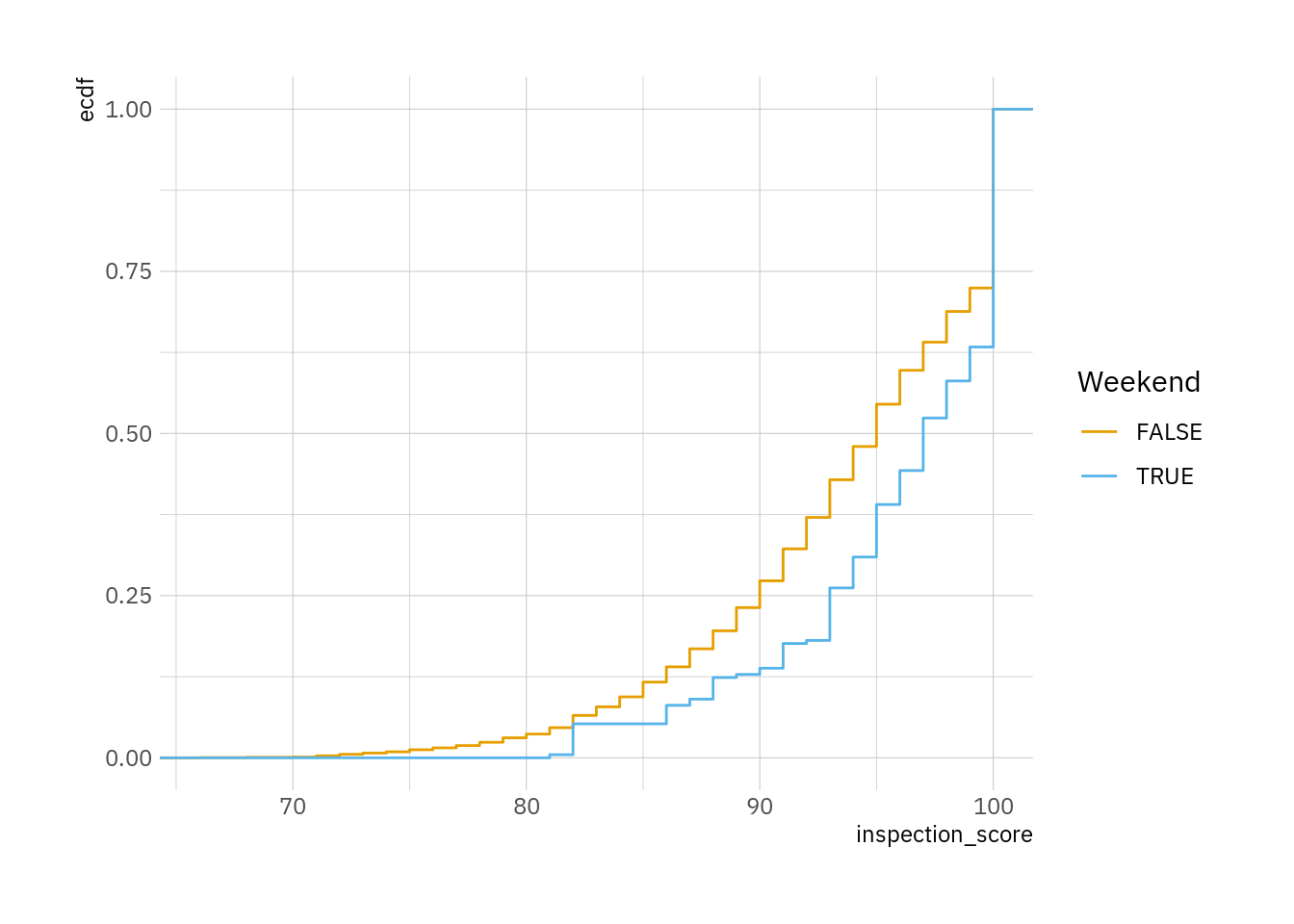
The graph above suggests that restaurants inspected during the weekend tend to obtain higher scores than restaurants inspected during the week.
To see if this holds after controlling for observables we estimate a linear regression model with an interaction term to allow the coefficients on year and number of locations to vary between weekdays and weekends:
mod <- lm(inspection_score ~ Weekend * (Year + NumberofLocations), data = dat)
modelsummary(mod)| (1) | |
|---|---|
| (Intercept) | 225.651 |
| (12.472) | |
| WeekendTRUE | −55.462 |
| (130.256) | |
| Year | −0.065 |
| (0.006) | |
| NumberofLocations | −0.019 |
| (0.000) | |
| WeekendTRUE × Year | 0.028 |
| (0.065) | |
| WeekendTRUE × NumberofLocations | −0.009 |
| (0.008) | |
| Num.Obs. | 27178 |
| R2 | 0.069 |
| R2 Adj. | 0.069 |
| AIC | 174873.7 |
| BIC | 174931.2 |
| Log.Lik. | −87429.866 |
| F | 401.830 |
| RMSE | 6.04 |
Average predictions and contrasts
The interactions make this model a bit difficult to interpret. Using the marginaleffects package, we can easily compute more meaningful quantities.
To begin, we estimate average predicted scores for restaurants inspected, by subgroups of our variable of interest:
avg_predictions(mod, by = "Weekend")
Weekend Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
FALSE 93.6 0.0368 2546 <0.001 93.6 93.7
TRUE 95.7 0.4167 230 <0.001 94.9 96.5
Columns: Weekend, estimate, std.error, statistic, p.value, conf.low, conf.high Under the hood, avg_predictions() computed the predicted value for each of the observations in the original dataset, and took the average by subgroup. The difference between the predictions in the two rows above represents the combination of two phenomena: the conditional association between Weekend and inspection_score, but also the fact that the distribution of covariates is different for restaurants inspected during weekdays or weekends. This is analogous to what Chernozhukov, Fernández-Val, and Melly (2013) call the “structural” and the “compositional” effects.
An alternative approach is to compute average counterfactual predictions. We proceed in 3 steps:
- Replicate the full dataset twice, setting
Weekend=0in the first dataset andWeekend=1in the second, while holding all other covariates at their original values. - Estimate predicted outcomes in both datasets.
- Report the means in each dataset.
To do this, we can simply add a variables argument to the previous call:
avg_predictions(mod, variables = "Weekend", by = "Weekend")
Weekend Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
FALSE 93.6 0.0368 2546 <0.001 93.6 93.7
TRUE 94.8 0.4977 190 <0.001 93.8 95.8
Columns: Weekend, estimate, std.error, statistic, p.value, conf.low, conf.high Notice that the average counterfactual predictions are slightly different from our initial estimates. This is because we have now marginalized over exactly the same distribution of covariates in the weekday and weekend counterfactual groups.
We can compute these average predictions:
avg_predictions(mod,
variables = "Weekend",
by = "Weekend",
hypothesis = "revpairwise")
Term Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
TRUE - FALSE 1.18 0.499 2.36 0.018 0.202 2.16
Columns: term, estimate, std.error, statistic, p.value, conf.low, conf.high Equivalently,
avg_comparisons(mod, variables = "Weekend")
Term Contrast Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
Weekend TRUE - FALSE 1.18 0.499 2.36 0.018 0.202 2.16
Columns: term, contrast, estimate, std.error, statistic, p.value, conf.low, conf.high Regression on a quantile of the outcome
Above, we provided one-number summaries with a single focus on the mean. But instead of modelling the outcome on its natural scale, we could model the probability that the outcome for a given observation lies below some quantile threshold. For example, the 30th percentile of inspection_score is:
qtile <- quantile(dat$inspection_score, prob = .30)
qtile30%
91 We can predict the probability that any given observation will fall below that threshold using a logit model:
mod <- glm(inspection_score < qtile ~ Weekend * (Year + NumberofLocations), data = dat, family = binomial)
modelsummary(mod)| (1) | |
|---|---|
| (Intercept) | −35.138 |
| (4.806) | |
| WeekendTRUE | −41.335 |
| (72.576) | |
| Year | 0.017 |
| (0.002) | |
| NumberofLocations | 0.006 |
| (0.000) | |
| WeekendTRUE × Year | 0.020 |
| (0.036) | |
| WeekendTRUE × NumberofLocations | 0.017 |
| (0.007) | |
| Num.Obs. | 27178 |
| AIC | 30590.4 |
| BIC | 30639.7 |
| F | 174.844 |
| RMSE | 0.43 |
predictions(mod)
Estimate Pr(>|z|) 2.5 % 97.5 %
0.231 <0.001 0.223 0.239
0.286 <0.001 0.279 0.293
0.305 <0.001 0.297 0.314
0.269 <0.001 0.260 0.278
0.278 <0.001 0.270 0.286
--- 27168 rows omitted. See ?avg_predictions and ?print.marginaleffects ---
0.374 <0.001 0.362 0.386
0.374 <0.001 0.362 0.386
0.374 <0.001 0.362 0.386
0.374 <0.001 0.362 0.386
0.374 <0.001 0.362 0.386
Columns: rowid, estimate, p.value, conf.low, conf.high, inspection_score, Weekend, Year, NumberofLocations And we can estimate the average probability that inspection scores fall below 91:
avg_predictions(mod, by = "Weekend", type = "response")
Weekend Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
FALSE 0.273 0.00266 102.7 <0.001 0.2676 0.278
TRUE 0.138 0.02228 6.2 <0.001 0.0944 0.182
Columns: Weekend, estimate, std.error, statistic, p.value, conf.low, conf.high The average effect of Weekend on the probability that inspection_score falls below its 30th percentile value is:
avg_comparisons(mod, variables = "Weekend")
Term Contrast Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
Weekend TRUE - FALSE -0.0319 0.0424 -0.752 0.452 -0.115 0.0512
Columns: term, contrast, estimate, std.error, statistic, p.value, conf.low, conf.high Notice that this is very different from the contrast that we computed in the previous section.
Distribution regression
The “distribution regression” approach is just a repeated application of the strategy in the previous section. It allows us to measure the association between the predictor of interest and the outcome at different quantiles of the outcome. This approach is a simple and convenient alternative to quantile regression.
What makes distribution regression especially attractive is that since we can apply it by repeated application of simple regression models, it is easy to customize for specific quantities of interest or identification assumptions.
For example, we could define 4 distinct quantities of interest using marginaleffects function:
# Average predictions for Weekend=TRUE and Weekend=FALSE
# Covariates held at their subgroup-specific observed values
FUN_pred_observed <- function(x) avg_predictions(x, by = "Weekend")
# Average predictions for Weekend=TRUE and Weekend=FALSE
# Covariates held at counterfactual values, identical in both subgroups
FUN_pred_counterfactual <- function(x) avg_predictions(x, variables = "Weekend", by = "Weekend")
# Average predictions for Weekend=TRUE and Weekend=FALSE
# Covariates held at Year=2010 and NumberofLocations=30
FUN_pred_fixed <- function(x) avg_predictions(x,
by = "Weekend",
newdata = datagrid(Weekend = c(TRUE, FALSE), NumberofLocations = 30, Year = 2010))
# Average contrast between Weekend=TRUE and Weekend=FALSE
FUN_comp <- function(x) avg_comparisons(x, variables = "Weekend")Now we can apply these functions to a series of regression models with quantiles of inspection_score and plot the results:
distreg <- function(FUN) {
out <- NULL
for (qtile in 1:9 / 10) {
# find quantile value
threshold <- quantile(dat$inspection_score, prob = qtile, na.rm = TRUE)
# model with binary dependent variable
f <- inspection_score < threshold ~ Weekend * (Year + NumberofLocations)
model <- glm(f, data = dat, family = binomial)
# quantity of interest
tmp <- FUN(model)
# save quantile for plotting
tmp$quantiles <- qtile
out <- rbind(out, tmp)
}
if (!"Weekend" %in% colnames(out)) out[["Weekend"]] <- "Difference"
ggplot(out, aes(x = quantiles, y = estimate, ymin = conf.low, ymax = conf.high, fill = Weekend)) +
geom_ribbon(alpha = .3) +
geom_line()
}distreg(FUN_pred_observed)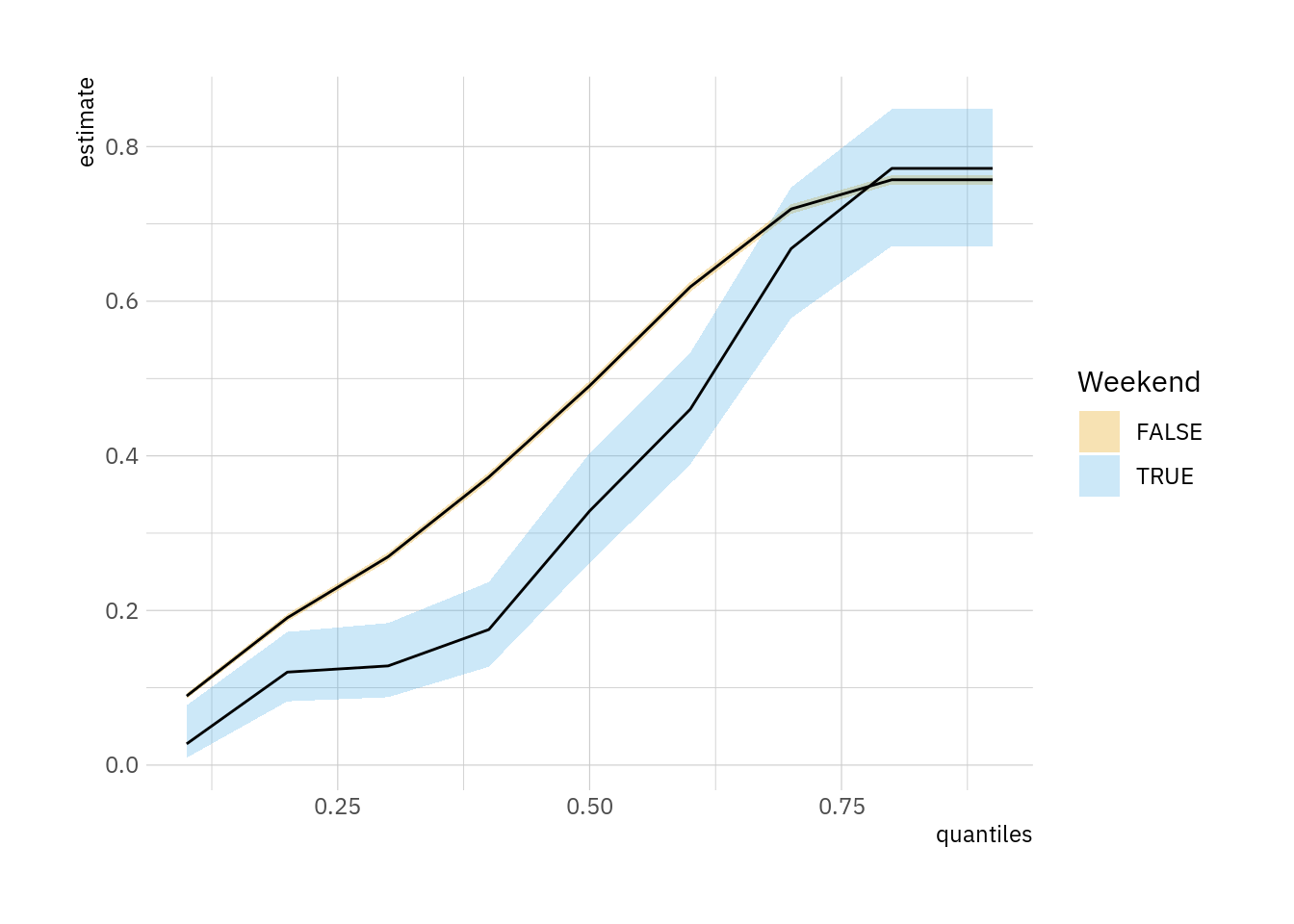
The curves above can be interpreted as CDFs. They suggest that when we hold covariates at subgroup-specific observed values, the probability of obtaining higher scores are greater on a weekend than on a weekday. This observation holds at all nearly all quantiles of the outcome variable, except at the very top of the evaluation scale, where the day of inspection does not appear to make a difference.
Note that the CDFs do vary quite a bit depending on the quantity of interest:
distreg(FUN_pred_counterfactual)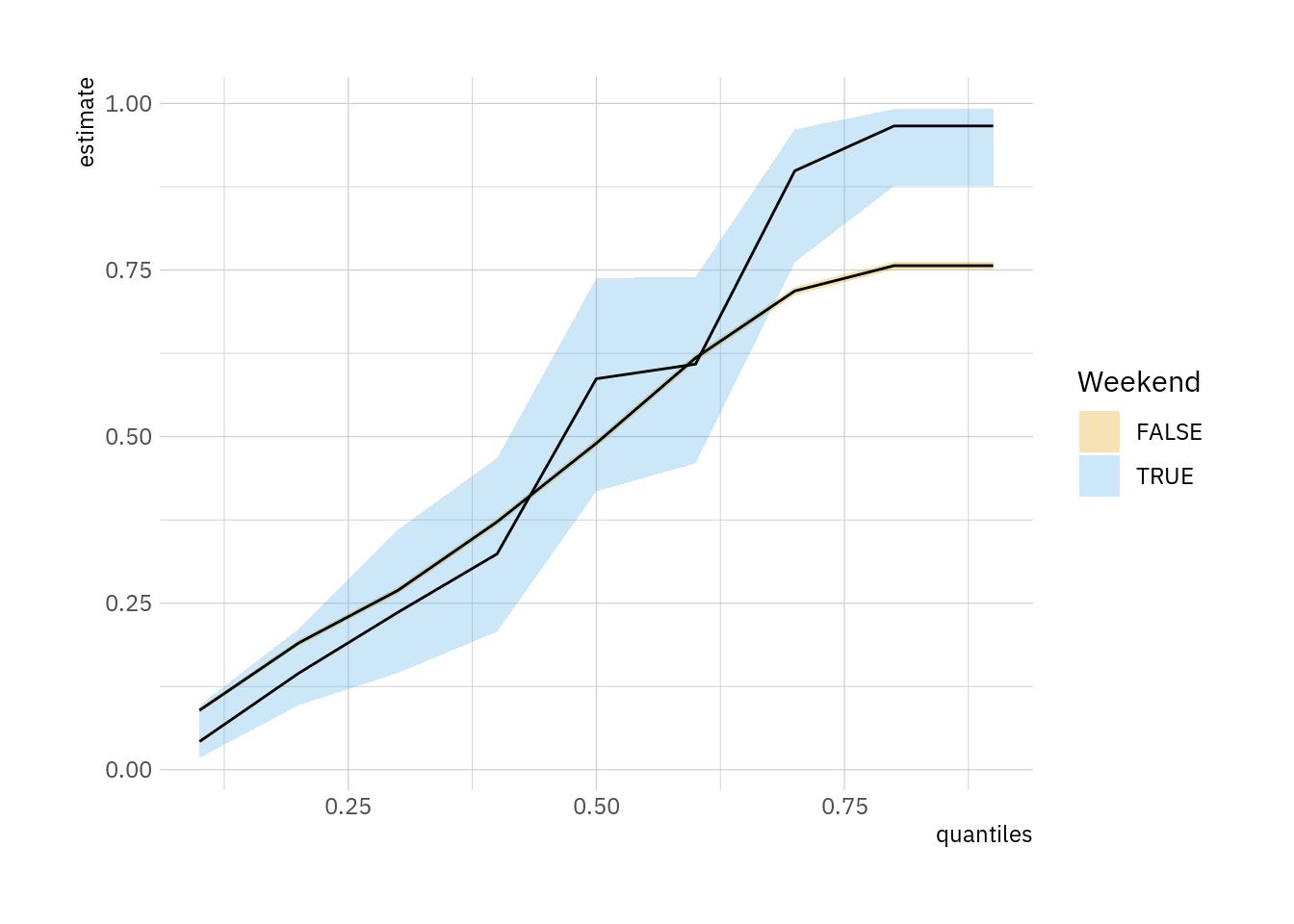
distreg(FUN_pred_fixed)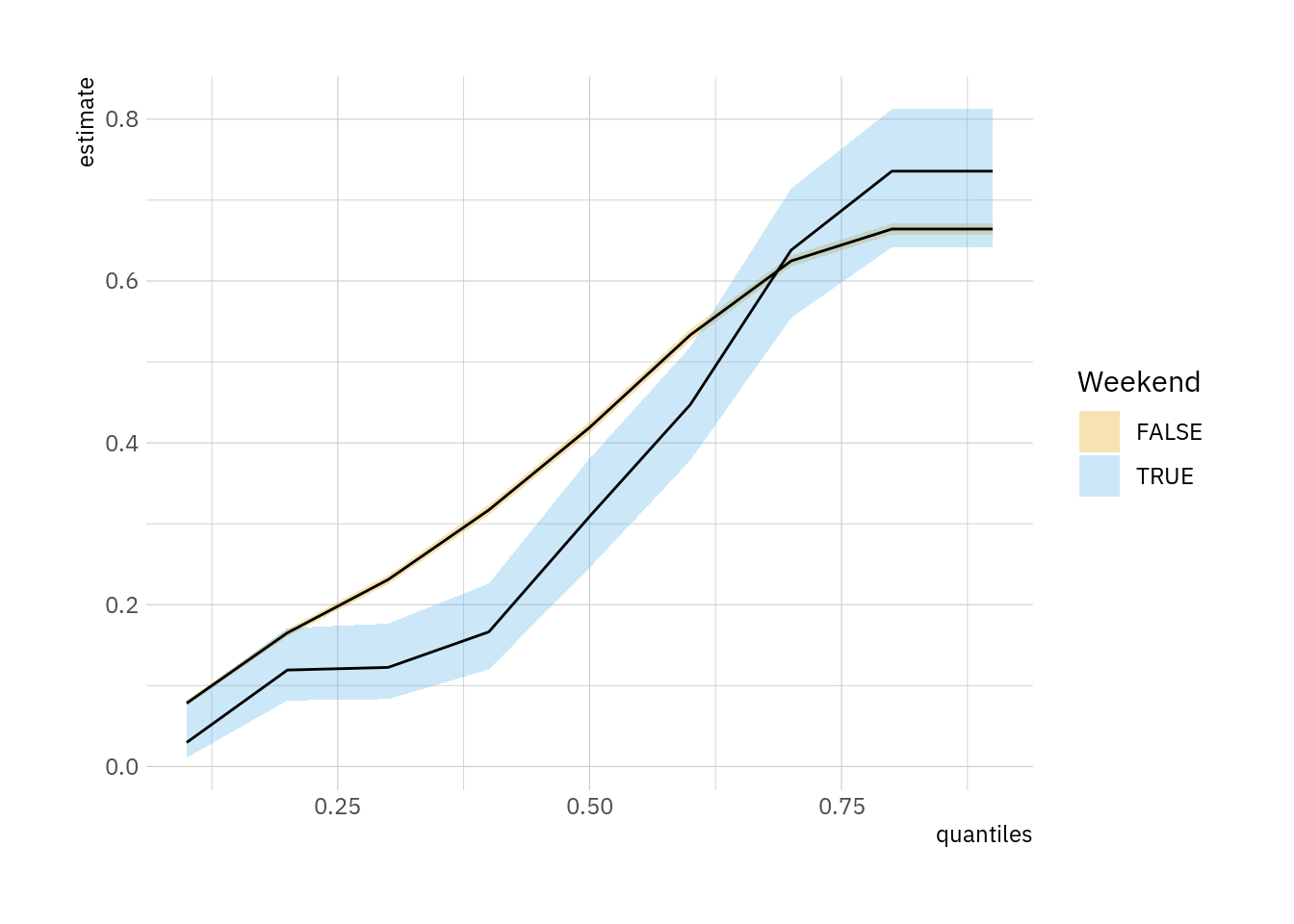
distreg(FUN_comp)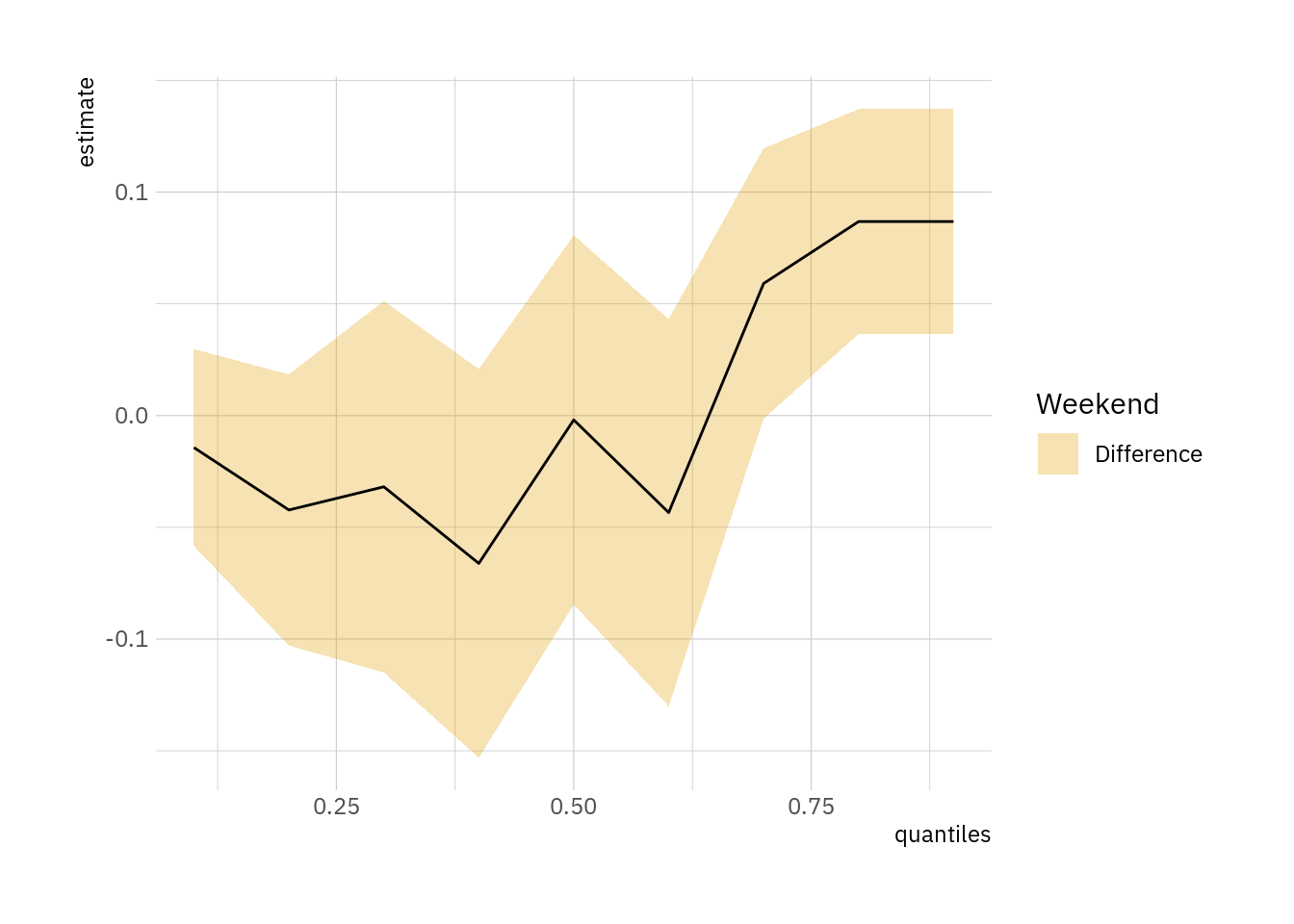
Going further
Chernozhukov, Fernández-Val, and Melly (2013) discuss inference for distribution regression, describe a bootstrap strategy, and explain how to construct simultaneous confidence sets.
Chernozhukov, Fernandez-Val, and Galichon (2007) explain how one can rearrange estimates to ensure that the CDF is weakly increasing. (h/t Apoorva Lal.)