This notebook offers an ultra-simple overview of Directed Acyclic Graphs (DAGs). My goal is to introduce readers who are unfamiliar with DAGs to tools which can help answer three critical questions:
- Is it possible to identify the effect of X on Y?
- What control variables do I need to include in my regression model?
- What control variables do I need to exclude from my regression model?
The presentation is informal; it privileges intuition over rigor. My target audiences are math-phobic students and researchers who want a quick introduction to the backdoor criterion.
I include several simulations in R. My experience is that these simulations reinforce intuitions.
This notebook is a translated copy of Chapter 6 from the French open access textbook that I published a couple years ago:
Arel-Bundock, Vincent. Analyse Causale et Méthodes Quantitatives: Une Introduction Avec R, Stata et SPSS. Presses de l’Université de Montréal, 2021. https://www.pum.umontreal.ca/catalogue/analyse_causale_et_methodes_quantitatives.
The translation was made entirely using Chat-GPT 4. I did not really check it. Please let me know if you find errors.
I may be willing to translate a few more chapters with DAGs and R simulations, covering topics like omitted variable bias, selection bias, and measurement error. Tell me if you are interested.
Introduction
The first part of the Arel-Bundock (2021) book introduces several descriptive analysis techniques, including visualization, univariate statistics, bivariate association measures, and linear regression. Unfortunately, the results produced by these techniques cannot automatically be interpreted causally, since causality is not a purely statistical or mathematical property. To determine whether a relationship is causal, we must complement the statistical analysis with a theoretical analysis.
This chapter introduces the directed acyclic graph (DAG), a tool that will help us identify the necessary conditions for giving a causal interpretation to statistical results. DAGs will also help us identify the control variables that must be included in a multiple regression model as well as those that must be excluded.
In his book Causality, Pearl (2000) introduces “Structural Causal Models” and shows how counterfactual comparisons can be graphically analyzed with a tool called the “directed acyclic graph.” DAGs offer a powerful and intuitive vocabulary for visually encoding our theories and research hypotheses.
To draw a DAG, an analyst must first mobilize their knowledge of the domain of study. This knowledge may be logically derived from a theory, informed by empirical analysis, or drawn from previous scientific studies. Based on this background knowledge, a researcher identifies the variables relevant to their theory and draws arrows to represent the causal relationships between each variable.
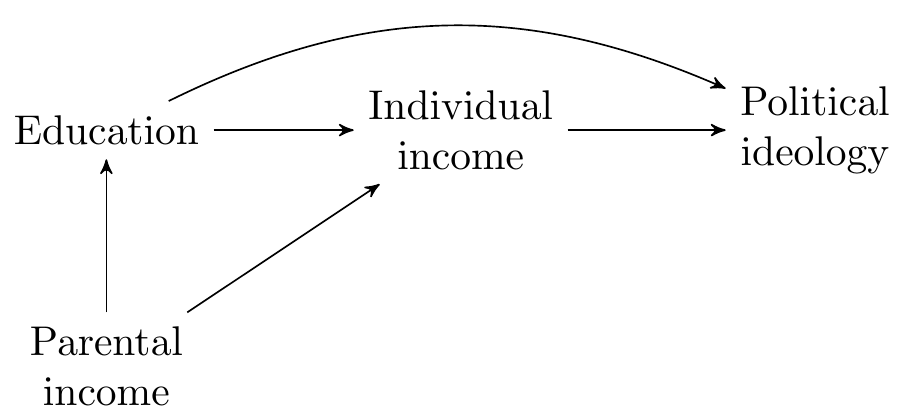
For example, imagine a researcher trying to measure the effect of education on political ideology. Previous studies suggest that, on average, (1) education increases individual income; (2) individual income increases support for political parties promising tax cuts; (3) parental income increases their children’s education; and (4) parental income increases their children’s income.
These causal relationships can be represented by the following DAG:
Drawing a DAG serves three main functions. First, any causal analysis necessarily relies on theoretical assumptions, not just mathematical or statistical relationships. Drawing a DAG forces the analyst to reveal their assumptions and research hypotheses explicitly and transparently.
Next, the formal techniques we will introduce in this chapter allow us to analyze a DAG and answer the following question: is it possible to identify the causal effect of the independent variable on the dependent variable?
Finally, studying a DAG allows us to identify the control variables that must be included in the multiple regression model as well as those that must be excluded.
Directed Acyclic Graphs
The first notable characteristic of a DAG is that it is a “directed” graph. A DAG is directed because the arrows that compose it indicate the direction of the causal relationship between variables.
In a DAG, causal relationships are always unidirectional.1 When drawing an arrow pointing from \(A\) to \(B\), we signal that \(A\) causes \(B\), not the reverse: \[\begin{align*} A \rightarrow B \end{align*}\]
When two causal relationships follow each other, we say they form a “path.” For example, if \(A\) causes \(B\) and \(B\) causes \(C\), we obtain the following path: \[\begin{align*} A \rightarrow B \rightarrow C \end{align*}\]
We say that a variable is the “descendant” of another variable if it is downstream in the path. We say that a variable is the “ancestor” of another variable if it is upstream in the path. In the example above, \(A\) and \(B\) are the ancestors of \(C\), while \(B\) and \(C\) are the descendants of \(A\).
In structural causal theory, \(A\) causes \(C\) if and only if \(A\) is an ancestor of \(C\). In other words, \(A\) causes \(C\) if and only if there is a path between \(A\) and \(C\) where all arrows point towards \(C\).
In this path, \(A\) causes \(C\): \[\begin{align*} A \rightarrow B \rightarrow C \end{align*}\]
In this path, \(A\) does not cause \(C\): \[\begin{align*} A \rightarrow B \leftarrow C \end{align*}\]
When there is no causal path between \(A\) and \(C\), it means that there is no causal relationship between these two variables. On average, an unbiased estimator of the causal effect of \(A\) on \(C\) should then produce an estimate equal to zero.
Directed Acyclic Graphs
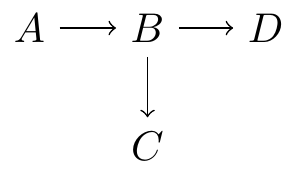
The second important characteristic of a DAG is that it is “acyclic”. In this context, the term “acyclic” means that the DAG does not contain a circular path that takes us back to the starting point, and where all arrows point in the same direction.
For example, this graph is a valid DAG, as it does not include a cycle:
This graph is not a valid DAG, as it includes a cycle:
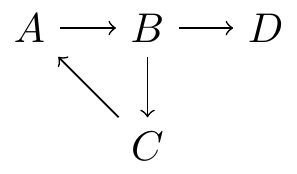
This characteristic of the DAG is important because the theoretical results that we will introduce later have only been mathematically proven in the context of acyclic graphs (Pearl 2000).
Causal Effect vs Statistical Information
To analyze a DAG, it is helpful to distinguish two phenomena: causal effect and statistical information.
Previously, we saw that a DAG can only represent a unidirectional causal effect. In a DAG, the causal effect flows from cause to effect, but never from effect to cause. In contrast, statistical information can flow in both directions. The cause can give us information about the effect, and the effect can give us information about the cause.2
Consider the following DAG:
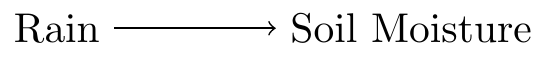
When it rains, the soil becomes moist. In this example, rain causes soil moisture and not the other way around. The causal relationship is unidirectional. However, if we see that the soil is moist, we can deduce that it rained recently. The moist soil gives us relevant information to deduce (or predict) whether there was rain in the last few hours. The effect gives us information about the cause. Even if causal relationships are always unidirectional, statistical information can sometimes flow in both directions.
Statistical information can also flow along more complex paths. For example, individuals with risky sexual behaviors are more likely to contract a sexually transmitted infection (STI) and experience a burning sensation during urination:

In this DAG, the relationship is unidirectional, going from “Risky Behavior” to “Infection” to “Burning”, in that order. However, statistical information flows in both directions.
The left end of the path allows us to better predict the right end of the path: individuals with risky sexual behavior are more likely to experience symptoms of an STI. A friend who notices Alexandre’s risky behavior warns him that he might feel a burning sensation soon.
The right end of the path allows us to better predict the left end of the path: individuals who experience a burning sensation during urination are more likely to have contracted an STI by engaging in risky activities. A doctor who notices that Alexandre experiences a burning sensation during urination asks him about his sexual behavior and recommends a blood test for screening.
When statistical information flows between \(A\) and \(C\), we say that the path between these two variables is “open”. When information does not flow between \(A\) and \(C\), we say that the path between these two variables is “closed”.
Typology of Paths
What determines whether a path is open or closed? To answer this question, we introduce a typology of paths. There are three basic causal structures:
The rest of this section describes the characteristics of these three types of paths. Two conclusions will be particularly important: (1) chains and forks are open, but colliders are closed; (2) when a regression model controls for the central link of a path, it reverses the flow of information: a closed path becomes open, and an open path becomes closed.
Fork: \(A \leftarrow B \rightarrow C\)
A fork is composed of a cause \(B\) and two effects \(A\) and \(C\). For example, a heatwave has two consequences: it raises the mercury level in the thermometer and increases ice cream sales.

A fork is open because statistical information flows between its two endpoints: the left endpoint of the fork allows us to better predict the right endpoint, and vice versa. When we see the mercury rise, we can predict that ice cream sales will increase. Conversely, if ice cream sales are high, we can predict that the mercury level in the thermometer is high. Observing one end of the fork gives us information about the other end. The fork is open.
In chapter \(\ref{sec:ols}\), we studied the linear regression model using least squares. This model allowed us to analyze data by “controlling” or “holding constant” certain variables. Intuitively, when we control a variable in a regression model, it is as if we fix that variable to a single constant and known value. Controlling a variable in a regression model is like observing that variable take a given value. This control has a decisive effect on the flow of information in a DAG.
Controlling the central link of a fork closes the path. For example, if we already know that the outside temperature is 35 °C, it is useless to look at the mercury to predict ice cream sales. If we already know the exact temperature, the height of the mercury column does not give us any additional information to better predict; knowing the central link of the fork is enough. When we fix the central link of a fork, the two endpoints no longer “communicate”.
Chain: \(A \rightarrow B \rightarrow C\)
A chain is a sequence of two causal relationships: \(A\) causes \(B\), and \(B\) causes \(C\). We have already considered an example of a chain in the previous section: risky sexual behaviors increase the likelihood of contracting an STI, and an infection increases the risk of feeling a burning sensation during urination.
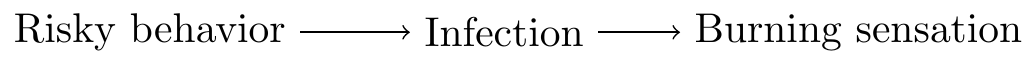
A chain is open because statistical information flows between its two endpoints: knowing the cause gives us relevant information to predict the effect, and knowing the effect gives us relevant information to predict the cause. Observing one end of the chain gives us information about the other end. The chain is open.
Controlling the central link of a chain closes the path. For example, Alexander’s doctor could directly measure the central link of the chain (“Infection”) by administering a blood test. Imagine that this test reveals that Alexander has not contracted an STI. After directly measuring the infection, the left endpoint of the chain no longer helps us predict the right endpoint of the chain. Knowing Alexander’s sexual habits does not help us predict whether he feels a burning sensation since the doctor already knows that Alexander has not contracted an STI. After directly measuring the infection, the right endpoint of the chain no longer helps us predict the left endpoint of the chain. Since the burning sensation is not linked to an STI, this symptom does not give us any clues to predict Alexander’s sexual behavior.
After observing the central link of a chain, the effect no longer helps us predict the cause. When we fix the central link of a chain, its two endpoints no longer “communicate”. When we control the variable in the middle of a chain, the path becomes closed.
Collider: \(A \rightarrow B \leftarrow C\)
A collider is composed of two variables \(A\) and \(C\) that contribute to causing the same effect \(B\). For example, a hockey team is more likely to win if it plays well and if the referee is biased in its favor.

A collider is closed because statistical information does not flow between its two endpoints. The fact that a referee is biased in favor of a team does not give us any information about the quality of the team’s play.3 Likewise, a team’s performance tells us little about the potential bias of the referee. Observing one end of the collider does not give us any information about the other end. The path is closed.
Controlling the central link of a collider opens the path. If we know that a team won even though they played poorly, the chances that the referee was biased are higher. On the other hand, if we know that a team won even though the referee was not biased, the chances that the team played well are higher. Knowing the central link of a collider allows us to make the connection between its endpoints. When we fix the central link, the two endpoints “communicate”.
Forks, chains, and collisions
In summary, the three causal structures have the following properties: \[\begin{align*} A \leftarrow B \rightarrow C && \mbox{Open} \\ A \rightarrow B \rightarrow C && \mbox{Open} \\ A \rightarrow B \leftarrow C && \mbox{Closed} \end{align*}\]
When the analyst controls for a variable in a multiple regression model, we draw a frame around the variable. For example, if the analyst controls for variable \(B\), we write: \(\boxed{B}\). As we have already seen, a statistical model that controls for the central link of the path reverses the flow of information: the fork and the chain become closed, and the collision becomes open: \[\begin{align*} A \leftarrow \boxed{B} \rightarrow C && \mbox{Closed} \\ A \rightarrow \boxed{B} \rightarrow C && \mbox{Closed} \\ A \rightarrow \boxed{B} \leftarrow C && \mbox{Open} \end{align*}\]
Finally, it is useful to highlight a counterintuitive phenomenon: controlling the descendant of a collision opens the path. For example, in the following DAG, the path between \(A\) and \(C\) is closed by the collision \(A\rightarrow B\leftarrow C\). However, if we control \(D\), the flow of information is reversed, and the path between \(A\) and \(C\) becomes open:
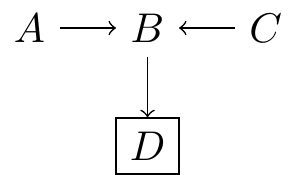
Combinations of forks, chains, and collisions
A path can be composed of several forks, chains, or collisions. A complex path is open if, and only if, all the links that make it up are open. As soon as a single link is closed, the path as a whole is closed.
For example, this path between \(A\) and \(E\) is open because all the links that make it up are forks or chains: \[\begin{align*} A \leftarrow B \leftarrow C \leftarrow D \rightarrow E && \mbox{Open} \end{align*}\]
In contrast, this path between \(A\) and \(E\) is closed because it contains a collision: \[\begin{align*} A \rightarrow B \leftarrow C \rightarrow D \rightarrow E && \mbox{Closed} \end{align*}\]
If at least one of the links in the path between \(A\) and \(E\) is closed, the entire path is closed. For example: \[\begin{align*} A \leftarrow B \leftarrow C \leftarrow \boxed{D} \rightarrow E && \mbox{Closed}\\ A \leftarrow \boxed{B} \leftarrow \boxed{C} \leftarrow \boxed{D} \rightarrow E && \mbox{Closed}\\ A \rightarrow \boxed{B} \leftarrow C \rightarrow D \rightarrow E && \mbox{Open} \end{align*}\]
Since controlling the descendant of a collision reverses the flow of information, this path is open:
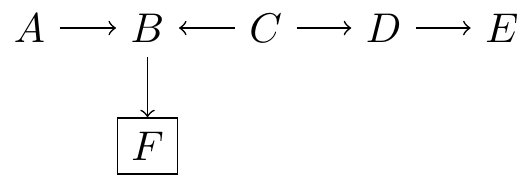
Causal Identification
We now have the necessary tools to dissect a DAG and determine under what conditions a statistical model allows for the identification of causal effects. The following two conditions are sufficient for the causal effect of \(X\) on \(Y\) to be identifiable:
- The statistical model does not control for a descendant of \(X\).
- All “backdoor paths” between \(X\) and \(Y\) are closed.
Identification condition 1 identifies the variables that should be excluded from a statistical model, and identification condition 2 identifies the control variables that should be included. We will now consider these two fundamental conditions in sequence.
Condition 1: Do not control for descendants of \(X\)
The first rule of causal identification is to avoid controlling for a variable that is downstream of the cause of interest (i.e., a descendant). In general, a statistical model that controls for a descendant of \(X\) will not identify the total causal effect of \(X\) on \(Y\).4
To understand the intuition behind this rule, consider a DAG representing a theoretical model of wage determination based on gender:
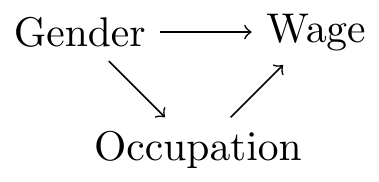
In this DAG, gender can have an effect on wages through two paths. First, there could be direct discrimination in wage determination. Second, there could be an indirect mechanism of structural discrimination that goes through occupation. For example, if women or transgender people are less likely to be promoted to management positions within a company, their wages will be lower. A study on discrimination “at comparable occupation,” that is, a statistical analysis that controls for the occupation of individuals, would ignore one of the main mechanisms that link gender and wages. In this type of study, the total causal effect of gender on wages is not identified.5
Condition 2: Close the backdoor paths
The second rule of causal identification is that all backdoor paths must be closed. A “backdoor path” is a path that meets two conditions:
- The path connects cause \(X\) to effect \(Y\).
- One end of the path points to \(X\).
Intuitively, a backdoor path represents “causes of the cause” (the path points to \(X\)). When factors determining the value of \(X\) are related to \(Y\) (the path is open), condition 2 of causal identification is violated, and it is impossible to estimate the causal effect of \(X\) on \(Y\).
To check if condition 2 of causal identification is met, proceed in three steps:
For example, imagine a researcher is interested in the causal effect of family breakdown (e.g., divorce) on the likelihood of a person becoming homeless:
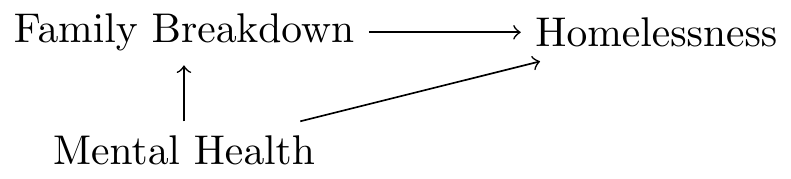
This DAG posits that family breakdown causes homelessness. It also suggests that a mental health disorder could be a common cause of the other two phenomena; this disorder could increase the likelihood of family breakdown and homelessness. This third factor opens a backdoor path between the cause and the effect of interest to the researcher. \[\begin{align*} \mbox{Family Breakdown} \leftarrow \boxed{\mbox{Mental Health}} \rightarrow \mbox{Homelessness} \end{align*}\]
To estimate the causal effect of family breakdown on homelessness, mental health disorders that could have caused the other two variables must be controlled. To estimate the causal effect, the backdoor path must be closed.
Intuitively, rule 2 of causal identification indicates how to eliminate spurious relationships or other possible explanations.
Examples
To illustrate how the rules of causal identification can be deployed in practice, we revisit the DAG with which we opened the chapter:
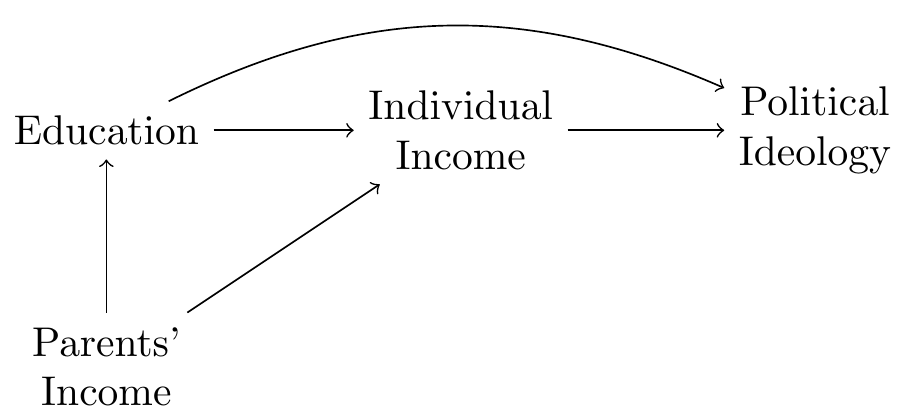
In this example, the researcher is trying to estimate the causal effect of “Education” on “Political Ideology”. Rule 1 of causal identification tells us not to control the descendants of the cause of interest. Therefore, our statistical model should not control the variable “Individual Income.”
Rule #2 of causal identification tells us to close all backdoor paths. In this case, there is a backdoor path between the cause and effect:

To close this path, we could control the variable “Parents’ Income” or the variable “Individual Income.” However, since “Individual Income” is a descendant of “Education,” controlling this variable would violate condition 1 of causal identification. Therefore, identifying the causal effect of “Education” on “Political Ideology” requires us to control the variable “Parents’ Income” and not control the variable “Individual Income.”
This strategy could be operationalized by a linear model: \[\begin{align*} \text{Ideology} = \beta_0 + \beta_1 \text{Education} + \beta_2 \text{Parents' Income} + \varepsilon \end{align*}\]
The next figure shows six additional examples. In each of these GOAs, the framed variables need to be controlled if we want to estimate the causal effect of \(X\) on \(Y\).
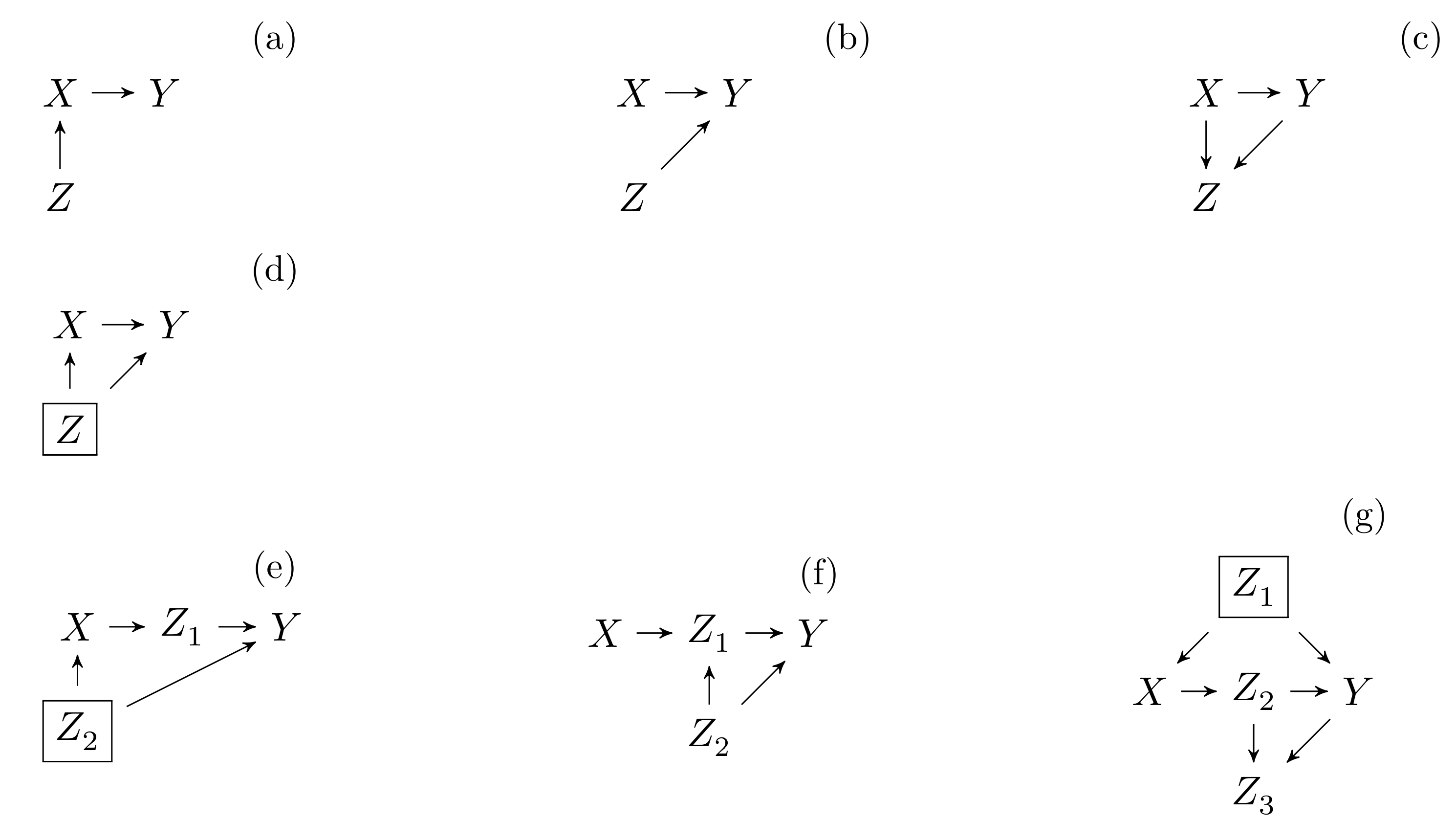
In panel (A), there is no backdoor path, so we don’t need to control anything. In order to estimate the causal effect of \(X\) on \(Y\), it is enough to measure the bivariate association between these variables.
In panel (B), there is no backdoor path. Once again, it is unnecessary to control for third factors; bivariate regression is sufficient.
In panel (C), there are two paths connecting \(X\) to \(Y\). First, there is the causal path of interest: \(X \rightarrow Y\). Next, there is a non-causal path: \(X \rightarrow Z \leftarrow Y\). This path is not a backdoor path since its end does not point into \(X\). Therefore, we don’t need to act to close this path. In fact, as \(Z\) is a descendant of \(X\), controlling \(Z\) would violate the first condition of causal identification.6
In panel (D), there is an open backdoor path: \(X \leftarrow Z \rightarrow Y\). It is therefore essential to control \(Z\) if we want to estimate the causal effect of \(X\) on \(Y\).
In panel (E), there is a backdoor path: \(X \leftarrow Z_2 \rightarrow Y\). In this context, it is essential to control \(Z_2\) if we want to estimate the causal effect of \(X\) on \(Y\). It is also important not to control \(Z_1\), as this variable is a descendant of \(X\).
In panel (F), there is no open backdoor path. The effect of \(X\) on \(Y\) is identifiable, even if we do not control any variables.
Panel (G) shows a slightly more complex theoretical model. In this model, three paths connect variables \(X\) and \(Y\): \[\begin{align*} X \rightarrow Z_2 \rightarrow Y \\ X \rightarrow Z_2 \rightarrow Z_3 \leftarrow Y\\ X \leftarrow Z_1 \rightarrow Y \end{align*}\]
In the first two paths, variables \(Z_2\) and \(Z_3\) are both descendants of \(X\). Following the first condition of causal identification, we know not to control these variables. The third path is open and ends with an arrow pointing towards \(X\). The second condition of causal identification states that it is essential to close this backdoor path by controlling \(Z_1\). To estimate the causal effect of \(X\) on \(Y\), we must therefore control \(Z_1\), but avoid controlling \(Z_2\) or \(Z_3\).
Lessons
Graphical causal analysis allows us to draw several practical lessons for the analysis of quantitative data and causal inference. In particular, causal graphs demonstrate the usefulness of randomized experiments, highlight the dangers associated with post-treatment bias, and reveal an important limitation of multiple regression models.
Randomized experiments
The second condition of causal identification shows why randomized experiments are often considered the “gold standard” for causal inference. If the treatment value is determined purely randomly, then the treatment has no ancestors. By construction, none of the arrows in the causal graph point to the cause, and there is no backdoor path. In an experiment where the treatment value is random, the second condition of causal identification is automatically satisfied. This is why randomized experiments are often considered a privileged method for studying causal relationships.
Post-treatment bias
The first condition of identification helps us understand a problem that many methodologists call “post-treatment bias.” This type of bias occurs when an analyst controls for a descendant of the cause. This violates the first condition of causal identification and risks introducing post-treatment bias. This type of bias can take two specific forms: closing a causal path and opening a non-causal path.
The first form of post-treatment bias is illustrated by this causal graph:
In this case, there are two causal paths through which variable \(X\) influences \(Y\): \(X\rightarrow Y\) and \(X\rightarrow Z\rightarrow Y\). The variable \(Z\) is posterior to the cause \(X\), as it is downstream in the causal chain. Controlling the variable \(Z\) in a regression model would close one of the two causal paths and produce a biased estimate of the “total” effect of \(X\) on \(Y\).7
Opening a non-causal path.
The second form of post-treatment bias is illustrated by this causal graph:
In this case, there is only one causal path between the two variables of interest: \(X \rightarrow Y\). The second path linking \(X\) and \(Y\) is non-causal since the arrows do not all point from \(X\) to \(Y\). Moreover, the path \(X \rightarrow Z \leftarrow Y\) is closed because it is a collision. However, if the analyst estimates a multiple regression model that controls for \(Z\), the non-causal path becomes open and allows statistical information to pass through: \(X \rightarrow \boxed{Z} \leftarrow Y\). This non-causal statistical information biases our estimate of the effect of \(X\) on \(Y\).
In general, we should avoid controlling for descendants of the cause we are interested in. Violating the first condition of identification risks introducing post-treatment bias and distorting our conclusions.
Interpretation of control variables
Causal graph analysis also helps develop an important reflex: in a multiple regression model, it is often preferable not to directly interpret the coefficients associated with control variables. In general, these coefficients do not estimate causal relationships. The following causal graph illustrates the problem well:
To identify the causal effect of \(X\) on \(Y\), we must close the backdoor path by controlling for \(Z\) (identification condition 2). To estimate the causal effect of \(X\) on \(Y\), we could estimate the following linear regression model: \[\begin{align} Y = \beta_0 + \beta_1 X + \beta_2 Z + \varepsilon \label{eq:interpret-controls} \end{align}\]
In contrast, to identify the causal effect of \(Z\) on \(Y\), we must avoid controlling for \(X\), since \(X\) is a descendant of \(Z\) (identification condition 1). To estimate the causal effect of \(Z\) on \(Y\), we could estimate the following linear regression model: \[\begin{align} Y = \alpha_0 + \alpha_1 Z + \nu \label{eq:interpret-controls2} \end{align}\]
The first model allows estimating the causal effect of \(X\), but not the causal effect of \(Z\). The second model allows estimating the causal effect of \(Z\), but not the causal effect of \(X\). In general, it is therefore prudent not to interpret the coefficients associated with control variables in a multiple regression model. Ideally, each research question should be tested using a separate model.
Simulations
To reinforce our intuition about the rules of causal identification, it is useful to proceed with simulations. The objective of this exercise is to create an artificial dataset that conforms exactly to the causal theory encoded by a DAG. Since we have created this dataset ourselves, we know precisely the true value of the causal effect that a good statistical model should estimate. We can thus compare the performance of different empirical approaches.
Simulation 1: Simple causal relationship
In the following model, an increase of one unit in \(X\) causes an increase of 1.7 units in \(Y\):
To create synthetic data that conforms to this model, we use the rnorm(n) function, which draws \(n\) random numbers from a normal distribution. Since \(X\) has no ancestors, this variable is purely random. \(Y\), on the other hand, is equal to \(1.7 \cdot X\), plus a random component:
n <- 100000
X <- rnorm(n)
Y <- 1.7 * X + rnorm(n)Un bon modèle statistique devrait estimer que l’effet causal de \(X\) sur \(Y\) est (approximativement) égal à 1,7. Comme prévu, le modèle de régression linéaire estime le bon coefficient:
mod <- lm(Y ~ X)
coef(mod) (Intercept) X
0.0003841575 1.7056832651 Simulation 2: Chain
The previous example consisted of a single causal relationship. When we study a chain of causal relationships, where each component of the chain is linear, the causal effect is equal to the product of the individual effects. For example, the true effect of \(X\) on \(Y\) in this DAG is \(3 \cdot 0.5 = 1.5\):
It is easy to verify this result by simulation:
X <- rnorm(n)
Z <- 3 * X + rnorm(n)
Y <- 0.5 * Z + rnorm(n)
mod <- lm(Y ~ X)
coef(mod) (Intercept) X
-0.003920851 1.497183730 Simulation 3: Collider
Now, consider a DAG with a collider:
We can simulate data that conforms to this DAG as follows:
X <- rnorm(n)
Y <- 1.7 * X + rnorm(n)
Z <- 1.2 * X + 0.8 * Y + rnorm(n)In this model, there is no backdoor path. Therefore, we do not need to control for anything. In fact, since \(Z\) is a descendant of \(X\), it is important not to control for this variable. The model without a control variable produces a good estimate of the causal effect of \(X\) on \(Y\), which is about 1.7:
mod <- lm(Y ~ X)
coef(mod) (Intercept) X
6.965923e-05 1.698331e+00 The model with the control variable produces a biased estimate of the causal effect of \(X\) on \(Y\), which is about 0.45:
mod <- lm(Y ~ X + Z)
coef(mod)(Intercept) X Z
0.001220143 0.449989450 0.487882145 Simulation 4: Fork
This DAG encodes relations between 4 variables:
These commands simulate data which conform to the DAG above:
Z2 <- rnorm(n)
X <- Z2 + rnorm(n)
Z1 <- 2 * X + rnorm(n)
Y <- 0.25 * Z1 + Z2 + rnorm(n)In this DAG, we need to close the backdoor path by controlling for \(Z_2\) and avoid controlling for the descendant \(Z_1\):
mod <- lm(Y ~ X + Z2)
coef(mod) (Intercept) X Z2
-0.007493872 0.495299482 1.009134033 Simulation 5: Complex Model
The following DAG reproduces the structure studied in panel (G).
This code simulates data that conforms to the theoretical model:
Z1 <- rnorm(n)
X <- Z1 + rnorm(n)
Z2 <- 2 * X + rnorm(n)
Y <- 0.5 * Z2 + Z1 + rnorm(n)
Z3 <- Z2 + Y + rnorm(n)Since we created this dataset ourselves, following exactly the relationships encoded in the DAG, we know that the true causal effect of \(X\) on \(Y\) in this data is equal to \(2 \cdot 0.5 = 1\). The theoretical analysis of the DAG that we conducted earlier also showed that an unbiased statistical model should include \(Z_1\), but exclude \(Z_2\) and \(Z_3\).
To verify the conclusion of our theoretical analysis, we estimate eight models with different combinations of the three control variables \(Z_1\), \(Z_2\), and \(Z_3\):
M1 <- lm(Y ~ X + Z1)
M2 <- lm(Y ~ X)
M3 <- lm(Y ~ X + Z2)
M4 <- lm(Y ~ X + Z3)
M5 <- lm(Y ~ X + Z1 + Z2)
M6 <- lm(Y ~ X + Z1 + Z3)
M7 <- lm(Y ~ X + Z2 + Z3)
M8 <- lm(Y ~ X + Z1 + Z2 + Z3)The next table shows the results of these eight models. As expected, the model with control over the variable \(Z_1\) only is accurate (coefficient of 1 for the variable \(X\)). On the other hand, the other seven models produce incorrect results. Choosing the right variables to include and exclude from our statistical model is crucial.
| Coefficients | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 |
|---|---|---|---|---|---|---|---|---|
| Constant | -0.0 | 0.0 | 0.0 | -0.0 | -0.0 | -0.0 | -0.0 | -0.0 |
| \(X\) | 1.0 | 1.5 | 0.5 | -0.2 | 0.0 | -0.2 | 0.2 | -0.0 |
| \(Z_1\) | 1.0 | 1.0 | 0.6 | 0.5 | ||||
| \(Z_2\) | 0.5 | 0.5 | -0.4 | -0.2 | ||||
| \(Z_3\) | 0.5 | 0.4 | 0.6 | 0.5 |
References
Footnotes
Chapter \(\ref{sec:endogeneity}\) discusses bidirectional causality.↩︎
More formally, we say that statistical information flows between two variables \(A\) and \(C\) if observing the value of \(A\) changes our estimate of \(P(C=c)\), and if observing the value of \(C\) changes our estimate of \(P(A=a)\).↩︎
This requires that referees do not systematically try to help winning or losing teams.↩︎
Sometimes, when a descendant is not on a path that connects cause \(X\) to effect \(Y\), controlling for this variable will not affect the estimates produced by our model. This control would then be harmless but unnecessary.↩︎
In chapter \(\ref{sec:mediation}\), we will see how to study “partial” effects, which we will then call “direct” and “indirect” effects.↩︎
Since \(X\rightarrow Z \leftarrow Y\) is a collider, controlling \(Z\) would open the flow of information on this non-causal path and bias our results.↩︎
For more details on the concept of “total” effect, see the chapter on mediation analysis \(\ref{sec:mediation}\).↩︎