Prior Predictive Checks with marginaleffects and brms

Author

Vincent Arel-Bundock

Published

May 1, 2023

Bayesians often advocate for the use of prior predictive checks (Gelman et al. 2020). The idea is to simulate from the model, without using the data, in order to refine the model before fitting. For example, we could draw parameter values from the priors, and use the model to simulate values of the outcome. Then, could inspect those to determine if the simulated outcomes (and thus the priors) make sense substantively. Prior predictive checks allow us to iterate on the model without looking at the data multiple times.

One major challenge lies in interpretation: When the parameters of a model are hard to interpret, the analyst will often need to transform before they can assess if the generated quantities make sense, and if the priors are an appropriate representation of available information.

In this post I show how to use the marginaleffects and brms packages for R to facilitate this process. The benefit of the approach described below is that it allows us to conduct prior predictive checks on the actual quantities of interest. For example, if the ultimate quantity that we want to estimate is a contrast or an Average Treatment Effect, then we can use marginaleffects to simulate the specific quantity of interest using just the priors and the model.

In this example, we create two model objects with brms. In one of them, we set sample_prior="only" to indicate that we do not want to use the dataset at all, and that we only want to use the priors and model for simulation:

library(brms)
library(ggplot2)
library(marginaleffects)
library(modelsummary)
options(brms.backend = "cmdstanr")
theme_set(theme_minimal())

titanic <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/Stat2Data/Titanic.csv")
titanic <- subset(titanic, PClass != "*")

f <- Survived ~ SexCode + Age + PClass

mod_prior <- brm(f,
    data = titanic,
    prior = c(prior(normal(0, .2), class = b)),
    cores = 4,
    sample_prior = "only")

mod_posterior <- brm(f,
    data = titanic,
    cores = 4,
    prior = c(prior(normal(0, .2), class = b)))

Now, we use the avg_comparisons() function from the marginaleffects package to compute contrasts of interest:

cmp <- list(
    "Prior" = avg_comparisons(mod_prior),
    "Posterior" = avg_comparisons(mod_posterior))

Finally, we compare the results with and without the data in tables and plots:

modelsummary(
    cmp,
    output = "markdown",
    statistic = "conf.int",
    fmt = fmt_significant(2),
    gof_map = NA,
    shape = term : contrast ~ model)
Prior Posterior
Age +1 0.005 -0.0058
[-0.391, 0.396] [-0.0080, -0.0037]
PClass 2nd - 1st -0.00099 -0.19
[-0.39570, 0.39466] [-0.27, -0.12]
PClass 3rd - 1st 0.0036 -0.38
[-0.3841, 0.3907] [-0.45, -0.31]
SexCode 1 - 0 0.0072 0.49
[-0.3933, 0.3916] [0.44, 0.55] 
draws <- lapply(names(cmp), \(x) transform(get_draws(cmp[[x]]), Label = x))
draws <- do.call("rbind", draws)

ggplot(draws, aes(x = draw, color = Label)) +
    xlim(c(-1, 1)) +
    geom_density() +
    facet_wrap(~term + contrast, scales = "free")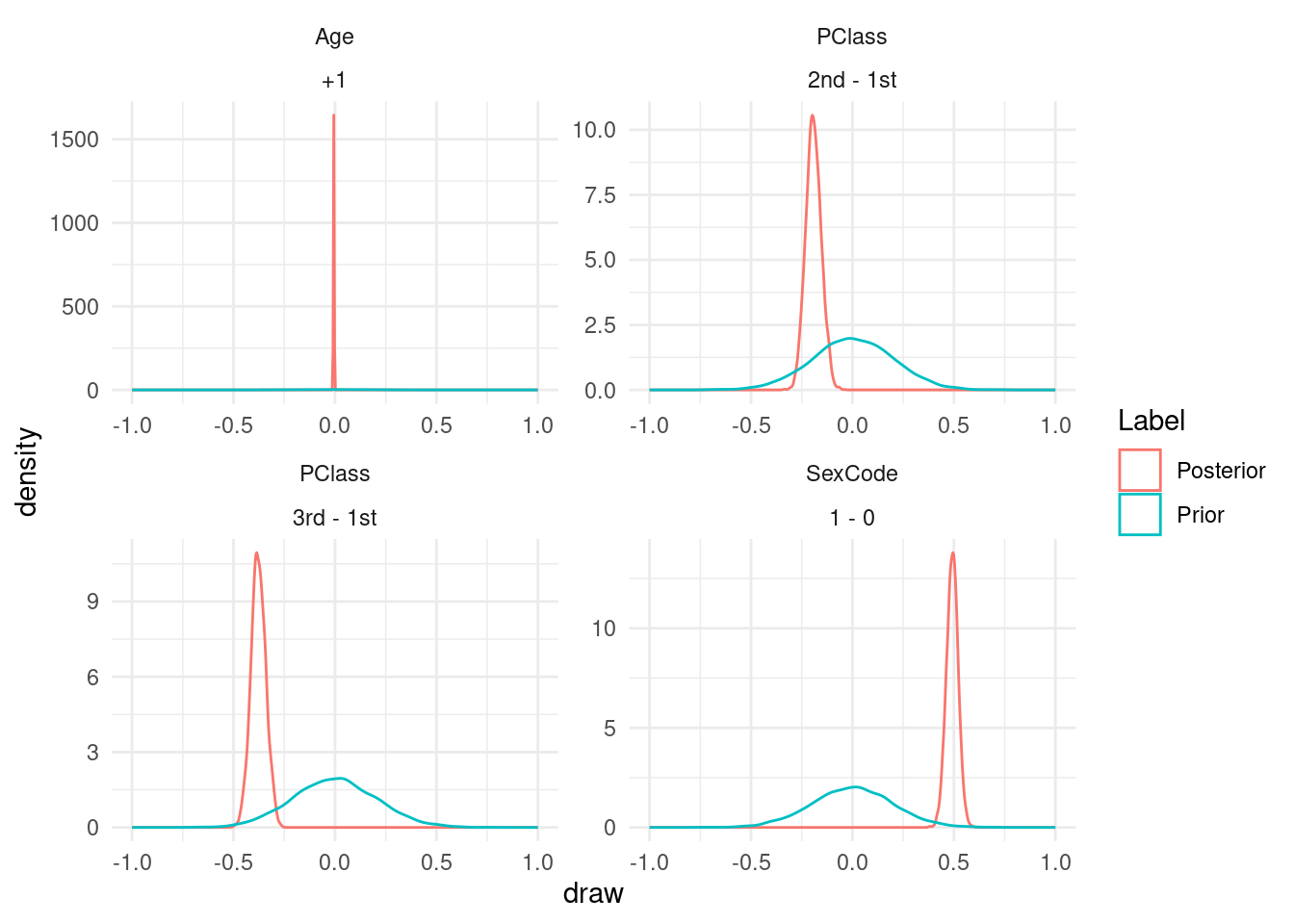

This kind of approach is particularly useful with more complicated models, such as this one with categorical outcomes. In such models, it would be hard to know if a normal prior is appropriate for the different parameters:

modcat_posterior <- brm(
    PClass ~ SexCode + Age,
    prior = c(
        prior(normal(0, 3), class = b, dpar = "mu2nd"),
        prior(normal(0, 3), class = b, dpar = "mu3rd")),
    family = categorical(link = logit),
    cores = 4,
    data = titanic)

modcat_prior <- brm(
    PClass ~ SexCode + Age,
    prior = c(
        prior(normal(0, 3), class = b, dpar = "mu2nd"),
        prior(normal(0, 3), class = b, dpar = "mu3rd")),
    family = categorical(link = logit),
    sample_prior = "only",
    cores = 4,
    data = titanic)
pd <- get_draws(comparisons(modcat_prior))

comparisons(modcat_prior) |> summary()
     rowid           term              group             contrast        
 Min.   :  1.0   Length:4536        Length:4536        Length:4536       
 1st Qu.:189.8   Class :character   Class :character   Class :character  
 Median :378.5   Mode  :character   Mode  :character   Mode  :character  
 Mean   :378.5                                                           
 3rd Qu.:567.2                                                           
 Max.   :756.0                                                           
    estimate             conf.low            conf.high        
 Min.   :-3.546e-03   Min.   :-0.8241741   Min.   :0.0000188  
 1st Qu.: 0.000e+00   1st Qu.:-0.3322749   1st Qu.:0.0162391  
 Median : 0.000e+00   Median :-0.0947103   Median :0.0917383  
 Mean   : 4.690e-06   Mean   :-0.2005252   Mean   :0.2005384  
 3rd Qu.: 0.000e+00   3rd Qu.:-0.0157481   3rd Qu.:0.3328813  
 Max.   : 4.111e-03   Max.   :-0.0000197   Max.   :0.8134400  
  predicted_lo        predicted_hi         predicted            tmp_idx     
 Min.   :0.000e+00   Min.   :0.000e+00   Min.   :0.000e+00   Min.   :  1.0  
 1st Qu.:0.000e+00   1st Qu.:0.000e+00   1st Qu.:0.000e+00   1st Qu.:189.8  
 Median :1.017e-05   Median :1.466e-05   Median :1.017e-05   Median :378.5  
 Mean   :1.592e-02   Mean   :1.571e-02   Mean   :1.574e-02   Mean   :378.5  
 3rd Qu.:2.471e-03   3rd Qu.:2.550e-03   3rd Qu.:2.471e-03   3rd Qu.:567.2  
 Max.   :1.966e-01   Max.   :1.966e-01   Max.   :1.966e-01   Max.   :756.0  
    PClass             SexCode           Age       
 Length:4536        Min.   :0.000   Min.   : 0.17  
 Class :character   1st Qu.:0.000   1st Qu.:21.00  
 Mode  :character   Median :0.000   Median :28.00  
                    Mean   :0.381   Mean   :30.40  
                    3rd Qu.:1.000   3rd Qu.:39.00  
                    Max.   :1.000   Max.   :71.00  
comparisons(modcat_posterior) |> summary()
     rowid           term              group             contrast        
 Min.   :  1.0   Length:4536        Length:4536        Length:4536       
 1st Qu.:189.8   Class :character   Class :character   Class :character  
 Median :378.5   Mode  :character   Mode  :character   Mode  :character  
 Mean   :378.5                                                           
 3rd Qu.:567.2                                                           
 Max.   :756.0                                                           
    estimate             conf.low           conf.high          predicted_lo    
 Min.   :-1.407e-01   Min.   :-0.218159   Min.   :-0.065904   Min.   :0.02497  
 1st Qu.:-1.223e-02   1st Qu.:-0.039564   1st Qu.:-0.008224   1st Qu.:0.21641  
 Median : 5.173e-04   Median :-0.008402   Median : 0.005425   Median :0.29599  
 Mean   : 7.790e-06   Mean   :-0.034669   Mean   : 0.034797   Mean   :0.33287  
 3rd Qu.: 2.658e-02   3rd Qu.: 0.010558   3rd Qu.: 0.090094   3rd Qu.:0.45914  
 Max.   : 1.401e-01   Max.   : 0.051580   Max.   : 0.225256   Max.   :0.89558  
  predicted_hi       predicted          tmp_idx         PClass         
 Min.   :0.02701   Min.   :0.02529   Min.   :  1.0   Length:4536       
 1st Qu.:0.22373   1st Qu.:0.21641   1st Qu.:189.8   Class :character  
 Median :0.31450   Median :0.29850   Median :378.5   Mode  :character  
 Mean   :0.33275   Mean   :0.33283   Mean   :378.5                     
 3rd Qu.:0.42014   3rd Qu.:0.44022   3rd Qu.:567.2                     
 Max.   :0.90812   Max.   :0.89558   Max.   :756.0                     
    SexCode           Age       
 Min.   :0.000   Min.   : 0.17  
 1st Qu.:0.000   1st Qu.:21.00  
 Median :0.000   Median :28.00  
 Mean   :0.381   Mean   :30.40  
 3rd Qu.:1.000   3rd Qu.:39.00  
 Max.   :1.000   Max.   :71.00

References

Gelman, Andrew, Aki Vehtari, Daniel Simpson, Charles C. Margossian, Bob Carpenter, Yuling Yao, Lauren Kennedy, Jonah Gabry, Paul-Christian Bürkner, and Martin Modrák. 2020. “Bayesian Workflow.” https://arxiv.org/abs/2011.01808.